题目内容
解关于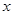 的不等式
的不等式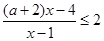 (其中
(其中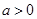 ).
).
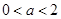 时,解集为
时,解集为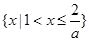 ;
;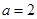 时,解集为
时,解集为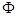 ;
;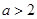 时,解集为
时,解集为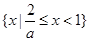 .
.
解析试题分析:(1)先将不等式整理成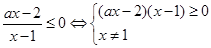 ,要解不等式
,要解不等式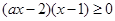 ,需要先解方程
,需要先解方程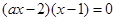
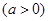 ,得两根
,得两根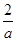 与
与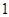 ,可以发现这两个根的大小不定,故此时需要对两根的大小进行比较即对参数
,可以发现这两个根的大小不定,故此时需要对两根的大小进行比较即对参数 进行分类讨论,从而确定不等式的解集.
进行分类讨论,从而确定不等式的解集.
试题解析:原不等式可化为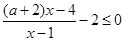 ,即
,即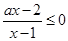 2分
2分
当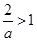 ,即
,即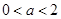 时,解集为
时,解集为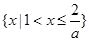 5分
5分
当 ,即
,即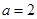 时,解集为
时,解集为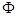 8分
8分
当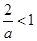 ,即
,即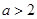 时,解集为
时,解集为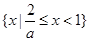 11分
11分
综上所述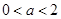 时,解集为
时,解集为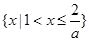 ;
;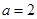 时,解集为
时,解集为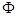 ;
;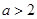 时,解集为
时,解集为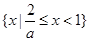 12分.
12分.
考点:1.含参不等式的求解问题;2.分类讨论的思想.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
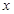 的不等式
的不等式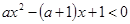
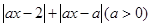 .
.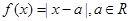 .
.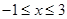 时,
时,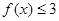 ,求a的取值范围;
,求a的取值范围;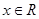 ,
,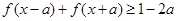 恒成立,求实数a的最小值.
恒成立,求实数a的最小值.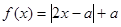 .
.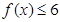 的解集为
的解集为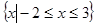 ,求实数a的值;(5分)
,求实数a的值;(5分)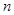 使
使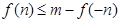 成立,求实数
成立,求实数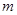 的取值范围.(5分)
的取值范围.(5分) 不等式
不等式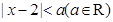 的解集为
的解集为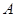 ,且
,且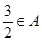 ,
,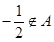 .
.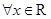 ,
,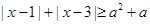 恒成立,且
恒成立,且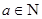 ,求
,求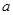 的值;
的值;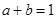 ,求
,求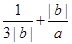 的最小值并指出取得最小值时
的最小值并指出取得最小值时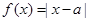 .
.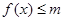 的解集为
的解集为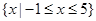 ,求实数
,求实数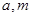 的值.
的值.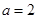 且
且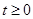 时,解关于
时,解关于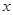 的不等式
的不等式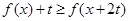 .
. ,关于
,关于 的不等式
的不等式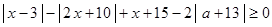 的解集不是空集,求实数
的解集不是空集,求实数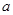 的取值范围.
的取值范围.