题目内容
已知递增等比数列{an}满足:a2+a3+a4=28,且a3+2是a2和a4的等差中项,
(Ⅰ) 求数列{an}的通项公式;
(Ⅱ)若bn=anlog
an,Sn=b1+b2+…+bn,求使Sn+n•2n+1>62成立的正整数n的最小值.
(Ⅰ) 求数列{an}的通项公式;
(Ⅱ)若bn=anlog
| 1 | 2 |
分析:(I)由题意,得
,由此能求出数列{an}的通项公式.
(Ⅱ)bn=anlog
an=2n•log
2n=-n•2n,Sn=b1+b2+…+bn=-(1×2+2×22+…+n×2n),所以数列{bn}的前项和Sn=2n+1-2-n•2n+1,使Sn+n•2n+1>62成立的正整数n的最小值.
|
(Ⅱ)bn=anlog
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(I)由题意,得
,…(2分)
解得
或
…(4分)
由于{an}是递增数列,所以a1=2,q=2
即数列{an}的通项公式为an=2•2n-1=2n…(6分)
(Ⅱ)bn=anlog
an=2n•log
2n=-n•2n…(8分)
Sn=b1+b2+…+bn=-(1×2+2×22+…+n×2n)①
则2Sn=-(1×22+2×23+…+n×2n+1)②
②-①,得Sn=(2+22+…+2n)-n•2n+1=2n+1-2-n•2n+1
即数列{bn}的前项和Sn=2n+1-2-n•2n+1…(10分)
则Sn+n•2n+1=2n+1-2>62,所以n>5,
即n的最小值为6.…(12分)
|
解得
|
|
由于{an}是递增数列,所以a1=2,q=2
即数列{an}的通项公式为an=2•2n-1=2n…(6分)
(Ⅱ)bn=anlog
| 1 |
| 2 |
| 1 |
| 2 |
Sn=b1+b2+…+bn=-(1×2+2×22+…+n×2n)①
则2Sn=-(1×22+2×23+…+n×2n+1)②
②-①,得Sn=(2+22+…+2n)-n•2n+1=2n+1-2-n•2n+1
即数列{bn}的前项和Sn=2n+1-2-n•2n+1…(10分)
则Sn+n•2n+1=2n+1-2>62,所以n>5,
即n的最小值为6.…(12分)
点评:本题考查数列的性质的应用,解题时要认真审题,注意数列与不等式的综合运用,合理地进行等价转化.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目


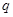 是等比数列
是等比数列 的公比,则“数列
的公比,则“数列 ”的既不充分也不必要条件;
”的既不充分也不必要条件; 上的函数
上的函数 是奇函数,则对定义域内的任意
是奇函数,则对定义域内的任意 必有
必有 ;
; 满足
满足 ,则
,则 的一个正周期为
的一个正周期为 ;
; 与
与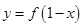 图像关于
图像关于 对称.
对称. 满足
满足 和
和 ,则
,则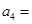
 D、8或
D、8或