题目内容
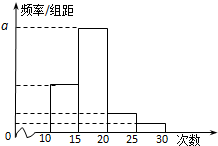
对某校高二年级学生参加社区服务的次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图(如图):
(Ⅰ)请写出表中M,m,n,p及图中a的值;
(Ⅱ)请根据频率分布直方图估计这M名学生参加社区服务的平均次数;
(Ⅲ)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求恰有一人参加社区服务次数落在区间M内的概率.
| 分组 | 频数 | 频率 |
| [10,15) | 10 | n |
| [15,20) | 26 | 0.65 |
| [20,25) | 3 | p |
| [25,30) | m | 0.025 |
| 合计 | M | 1 |
(Ⅱ)请根据频率分布直方图估计这M名学生参加社区服务的平均次数;
(Ⅲ)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求恰有一人参加社区服务次数落在区间M内的概率.

(Ⅰ)由分组[15,20)内的频数是26,频率是0.65知,
=0.65,所以M=40
因为频数之和为40,所以10+26+3+m=40,m=1,n=
=0.25,p=
=
=0.075,
因为a是对应分组[15,20)的频率与组距的商,所以a=
=0.13;
(Ⅱ)由(Ⅰ)得分组[10,15)内的频率为0.25,分组[15,20)内的频率为0.65,分组[20,25)内的频率为0.075,分组[25,30)内的频率为0.025M名学生参加社区服务的平均次数为12.5×0.25+17.5×065+22.5×0075+
275×0025=3.125+11.375+1.6875+0.6875=16.875≈17
所以估计M名学生参加社区服务的平均次数为17;
(Ⅲ)这个样本中,参加社区服务次数不少于20次的学生共有m+1=4人
设在区间[20,25)内的人为a1,a2,a3,在区间[25,30)内的人为b,
则任选2人共6种情况:
(a1,a2),(a1,a3),(a2,a3),(a1,b),(a2,b),(a3,b),
恰有一人参加社区服务次数在区间[25,30)内的情况共有3种:(a1,b),(a2,b),(a3,b)
所以,恰有一人参加社区服务次数在区间M内的概率为p=
=
.
| 26 |
| M |
因为频数之和为40,所以10+26+3+m=40,m=1,n=
| 10 |
| 40 |
| 3 |
| M |
| 3 |
| 40 |
因为a是对应分组[15,20)的频率与组距的商,所以a=
| 0.65 |
| 5 |
(Ⅱ)由(Ⅰ)得分组[10,15)内的频率为0.25,分组[15,20)内的频率为0.65,分组[20,25)内的频率为0.075,分组[25,30)内的频率为0.025M名学生参加社区服务的平均次数为12.5×0.25+17.5×065+22.5×0075+
275×0025=3.125+11.375+1.6875+0.6875=16.875≈17
所以估计M名学生参加社区服务的平均次数为17;
(Ⅲ)这个样本中,参加社区服务次数不少于20次的学生共有m+1=4人
设在区间[20,25)内的人为a1,a2,a3,在区间[25,30)内的人为b,
则任选2人共6种情况:
(a1,a2),(a1,a3),(a2,a3),(a1,b),(a2,b),(a3,b),
恰有一人参加社区服务次数在区间[25,30)内的情况共有3种:(a1,b),(a2,b),(a3,b)
所以,恰有一人参加社区服务次数在区间M内的概率为p=
| 3 |
| 6 |
| 1 |
| 2 |

练习册系列答案
相关题目