题目内容
如图,2012年春节,摄影爱好者S在某公园A处,发现正前方B处有一立柱,测得立柱顶端O的仰角和立柱底部B的俯角均为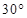 ,已知S的身高约为
,已知S的身高约为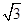 米(将眼睛距地面的距离按
米(将眼睛距地面的距离按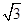 米处理)
米处理)
(1) 求摄影者到立柱的水平距离和立柱的高度;
(2) 立柱的顶端有一长2米的彩杆MN绕中点O在S与立柱所在的平面内旋转.摄影者有一视角范围为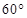 的镜头,在彩杆转动的任意时刻,摄影者是否都可以将彩杆全部摄入画面?说明理由.
的镜头,在彩杆转动的任意时刻,摄影者是否都可以将彩杆全部摄入画面?说明理由.
(1) 摄影者到立柱的水平距离为3米,立柱高为 米. (2) 摄影者可以将彩杆全部摄入画面.
米. (2) 摄影者可以将彩杆全部摄入画面.
解析试题分析:(1) 如图,不妨将摄影者眼部设为S点,做SC垂直OB于C,
又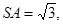 故在
故在 中,可求得BA=3,即摄影者到立柱的水平距离为3米……… 3分
中,可求得BA=3,即摄影者到立柱的水平距离为3米……… 3分
由SC=3, 在
在 中,可求得
中,可求得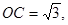
又 故
故 即立柱高为
即立柱高为 米. -------------- 6分
米. -------------- 6分
(2) (注:若直接写当 时,
时,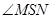 最大,并且此时
最大,并且此时 ,得2分)
,得2分)
连结SM,SN, 在△SON和△SOM中分别用余弦定理,
 ……8分
……8分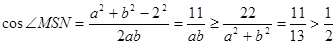

故摄影者可以将彩杆全部摄入画面. …………………………………………… 10分
考点:解三角形的实际应用;余弦定理。
点评:在解应用题时,分析题意,分清已知与所求,再根据 题意正确画出示意图,通过这一步可将实际问题转化为可用数学方法解决的问题。解题中,要注意正、余弦定理的应用。

练习册系列答案
相关题目
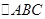 中,角
中,角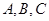 所对的边分别为
所对的边分别为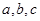 且满足
且满足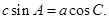
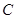 的大小;
的大小;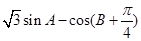 的最大值,并求取得最大值时角
的最大值,并求取得最大值时角 的大小.
的大小.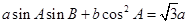 ,
,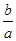 ;(2)当
;(2)当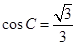 时,求
时,求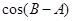 的值。
的值。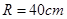 ,该车的底盘与轮胎中心在同一水平面上. 该车的涉水安全要求是:水面不能超过它的底盘高度. 如图所示:某处有一“坑形”地面,其中坑
,该车的底盘与轮胎中心在同一水平面上. 该车的涉水安全要求是:水面不能超过它的底盘高度. 如图所示:某处有一“坑形”地面,其中坑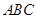 形成顶角为
形成顶角为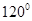 的等腰三角形,且
的等腰三角形,且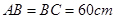 ,如果地面上有
,如果地面上有 (
(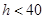 )高的积水(此时坑内全是水,其它因素忽略不计).
)高的积水(此时坑内全是水,其它因素忽略不计).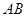 、
、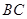 同时接触时,求证:此轮胎露在水面外的高度(从轮胎最上部到水面的距离)为
同时接触时,求证:此轮胎露在水面外的高度(从轮胎最上部到水面的距离)为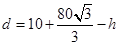 ;
;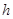 的最大值.
的最大值.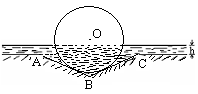
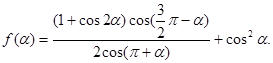
 的内角,且为钝角,求
的内角,且为钝角,求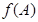 的最小值;
的最小值;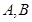 是锐角
是锐角 的内角,且
的内角,且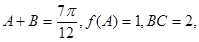 求
求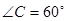 ,
,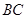 长度大于
长度大于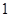 米,且
米,且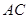 比
比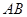 长
长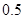 米,为了广告牌的稳固,要求
米,为了广告牌的稳固,要求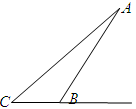
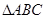 中,角
中,角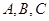 的对边分别是
的对边分别是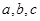 已知向量
已知向量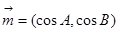
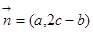 ,且
,且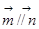 .
.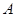 的大小;
的大小; 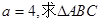 面积的最大值。
面积的最大值。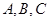 所对的分别是
所对的分别是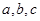 。已知
。已知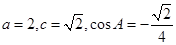 。(1)求
。(1)求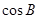 的值;
的值;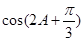 的值。
的值。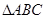 中,角
中,角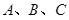 的对边分别为
的对边分别为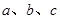 ,且
,且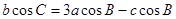 .
.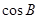 的值;
的值;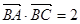 ,且
,且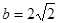 ,求
,求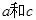 的值.
的值.