题目内容
函数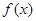 是定义域为
是定义域为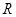 的奇函数,当
的奇函数,当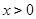 时
时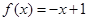 ,则当
,则当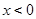 时,
时, 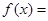
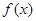 是定义域为
是定义域为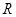 的奇函数,当
的奇函数,当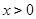 时
时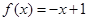 ,则当
,则当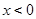 时,
时, 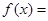
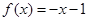
试题分析:因为函数
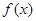 是定义域为
是定义域为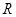 的奇函数,当
的奇函数,当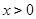 时
时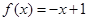 ,所以x=0时,f(x)=0;当x<0时,-x>0,所以f(x)=-f(-x)=-[-(-x)+1]=-x-1,故答案为
,所以x=0时,f(x)=0;当x<0时,-x>0,所以f(x)=-f(-x)=-[-(-x)+1]=-x-1,故答案为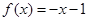 。
。点评:典型题,分段函数是高考考查的重点函数类型之一,能和许多常见函数结合在一起,也能和函数的奇偶性、单调性相结合。

练习册系列答案
相关题目
题目内容
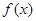 是定义域为
是定义域为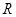 的奇函数,当
的奇函数,当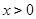 时
时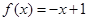 ,则当
,则当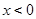 时,
时, 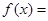
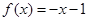
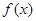 是定义域为
是定义域为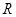 的奇函数,当
的奇函数,当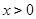 时
时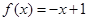 ,所以x=0时,f(x)=0;当x<0时,-x>0,所以f(x)=-f(-x)=-[-(-x)+1]=-x-1,故答案为
,所以x=0时,f(x)=0;当x<0时,-x>0,所以f(x)=-f(-x)=-[-(-x)+1]=-x-1,故答案为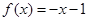 。
。