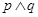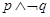题目内容
有下列四种说法:
①命题:“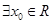 ,使得
,使得 ”的否定是“
”的否定是“ ,都有
,都有 ”;
”;
②已知随机变量 服从正态分布
服从正态分布 ,
, ,则
,则 ;
;
③函数 图像关于直线
图像关于直线 对称,且在区间
对称,且在区间 上是增函数;
上是增函数;
④设实数 ,则满足:
,则满足: 的概率为
的概率为 。其中错误的个数是 ( )
。其中错误的个数是 ( )
| A.0 | B.1 | C.2 | D.3。 |
A
解析试题分析:特称命题的否定是全称命题,所以①正确;由于随机变量 服从正态分布
服从正态分布 ,所以高整套分布的均值为1,
,所以高整套分布的均值为1,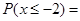

 ,故
,故 正确;
正确;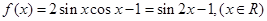 ,由
,由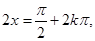
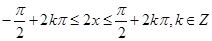 可得
可得 正确;由几何概率可知,实数
正确;由几何概率可知,实数 ,则满足:
,则满足: 的概率为
的概率为 ,所以
,所以 正确.故选A.
正确.故选A.
考点:1.命题的否定;2.正弦函数的性质;3.正态分布的性质.

练习册系列答案
相关题目
下列是全称命题并且是真命题的是
A.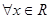 , ,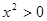 | B.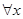 , ,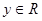 , ,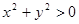 |
C.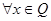 , ,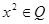 | D.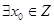 , ,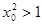 |
“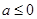 ”是“函数
”是“函数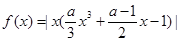 在区间
在区间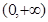 上单调递增”的( )
上单调递增”的( )
| A.充分必要条件 | B.必要不充分条件 |
| C.充分不必要条件 | D.既不充分也不必要条件 |
设向量 ,
,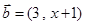 ,则“
,则“ ∥
∥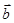 ”是“
”是“ ”的( )
”的( )
| A.充分非必要条件 | B.必要非充分条件 |
| C.充分必要条件 | D.既非充分又非必要条件 |
“|x-1|<2成立”是“x(x-3)<0成立”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
下列四个条件中,p是q的必要不充分条件的是 ( )
| A.p:a>b q:a2>b2 |
| B.p:a>b q:2a>2b |
| C.p:ax2+by2=c为双曲线 q:ab<0 |
D.p:ax2+bx+c>0 q: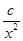 + +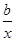 +a>0 +a>0 |
设 ,则“
,则“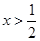 ”是“
”是“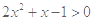 ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知命题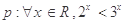 ,命题
,命题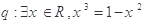 ,则下列命题中为真命题的是( )
,则下列命题中为真命题的是( )
A.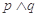 | B.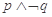 | C.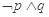 | D.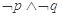 |
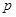 :函数
:函数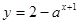 恒过(1,2)点;命题
恒过(1,2)点;命题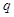 :若函数
:若函数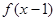 为偶函数,则
为偶函数,则 的图像关于直线
的图像关于直线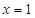 对称,则下列命题为真命题的是( )
对称,则下列命题为真命题的是( )