题目内容
20.已知函数f(x)=$\frac{1}{3}$x3+$\frac{1}{2}$ax2+bx+1(a,b∈R,且b≥-2)当x∈[-$\sqrt{2}$,$\sqrt{2}$]时,总有f′(x)≤0.(1)求函数f(x)的解析式;
(2)设函数g(x)=-3f(x)+mx2-6x(m∈R),求证:当x∈[0,1]时,若|g′(x)|≤1恒成立,则|g(x)|≤3.5也恒成立.
分析 (1)先求导f′(x)=x2+ax+b,从而可得$\left\{\begin{array}{l}{f′(-\sqrt{2})=2-a\sqrt{2}+b≤0}\\{f′(\sqrt{2})=2+\sqrt{2}a+b≤0}\end{array}\right.$,从而可求得b=-2,代回可得a=0;从而求出函数f(x)的解析式;
因此f(x)=$\frac{1}{3}$x3-2x+1.
(2)化简g(x)=-3($\frac{1}{3}$x3-2x+1)+mx2-6x=-x3+mx2-3,再求导可得g′(x)=-3x2+2mx,从而化当x∈[0,1]时,|g′(x)|≤1为$\left\{\begin{array}{l}{|g′(1)|=|-3+2m|≤1}\\{0≤\frac{m}{3}≤1}\\{|g′(m)=\frac{{m}^{2}}{3}≤1|}\end{array}\right.$或$\left\{\begin{array}{l}{|g′(1)|=|-3+2m|≤1}\\{\frac{m}{3}>1}\\{|g′(0)|=0≤1}\end{array}\right.$ 或$\left\{\begin{array}{l}{|g′(1)|=|-3+2m|≤1}\\{\frac{m}{3}<0}\\{|g′(0)|=0≤1}\end{array}\right.$;
从而解出1≤m≤$\sqrt{3}$;从而转化为证明1≤m≤$\sqrt{3}$时,|g(x)|≤3.5恒成立即可.
解答 解:(1)由题意得,f′(x)=x2+ax+b,
当x∈[-$\sqrt{2}$,$\sqrt{2}$]时,总有f′(x)≤0,
故$\left\{\begin{array}{l}{f′(-\sqrt{2})=2-a\sqrt{2}+b≤0}\\{f′(\sqrt{2})=2+\sqrt{2}a+b≤0}\end{array}\right.$,
化简可得,4+2b≤0,又∵b≥-2,
∴b=-2,
∴$\left\{\begin{array}{l}{2-\sqrt{2}a-2≤0}\\{2+\sqrt{2}a-2≤0}\end{array}\right.$,
解得,a=0;
因此f(x)=$\frac{1}{3}$x3-2x+1.
(2)证明:g(x)=-3($\frac{1}{3}$x3-2x+1)+mx2-6x=-x3+mx2-3,
g′(x)=-3x2+2mx是关于x的二次函数,
当x∈[0,1]时,|g′(x)|≤1可化为
$\left\{\begin{array}{l}{|g′(1)|=|-3+2m|≤1}\\{0≤\frac{m}{3}≤1}\\{|g′(m)=\frac{{m}^{2}}{3}≤1|}\end{array}\right.$或$\left\{\begin{array}{l}{|g′(1)|=|-3+2m|≤1}\\{\frac{m}{3}>1}\\{|g′(0)|=0≤1}\end{array}\right.$ 或$\left\{\begin{array}{l}{|g′(1)|=|-3+2m|≤1}\\{\frac{m}{3}<0}\\{|g′(0)|=0≤1}\end{array}\right.$;
解得,1≤m≤$\sqrt{3}$.
因此,当x∈[0,1]时,|g′(x)|≤1的恒成立,则1≤m≤$\sqrt{3}$;
由g′(x)=-3x2+2mx>0(0≤x≤1)可知,
当1≤m≤$\frac{3}{2}$时,g(x)在[0,$\frac{2m}{3}$]为增函数,在[$\frac{2m}{3}$,1]上为减函数,
|g(0)|=3≤3.5,|g(1)|=|m-4|≤3,|g($\frac{2m}{3}$)|=|$\frac{4{m}^{3}}{27}+3$|≤3.5,
即|g(x)|≤3.5;
当$\frac{3}{2}$≤m≤$\sqrt{3}$时,g(x)在[0,1]为增函数,
|g(0)|=3≤3.5,|g(1)|=|m-4|≤2.5,即|g(x)|≤3.5.
综上所述,当x∈[0,1]时,若|g′(x)|≤1恒成立,则|g(x)|≤3.5也恒成立.
点评 本题考查了导数的综合应用及恒成立问题,同时考查了分类讨论的思想应用,属于难题.

 阅读快车系列答案
阅读快车系列答案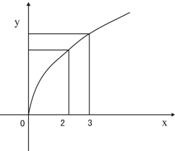 函数f(x)的图象如图,f′(x)是f(x)的导函数,则下列数值排列正确的是( )
函数f(x)的图象如图,f′(x)是f(x)的导函数,则下列数值排列正确的是( )| A. | 0<f′(2)<f′(3)<f(3)-f(2) | B. | 0<f(3)-f(2)<f′(2)<f′(3) | C. | 0<f′(3)<f′(2)<f(3)-f(2) | D. | 0<f′(3)<f(3)-f(2)<f′(2) |
| A. | [-e2,$\frac{1}{{e}^{2}}$] | B. | [-e2,$\frac{1}{{e}^{2}}$) | C. | [-e2,$\frac{1}{{e}^{2}}$)∪{$\frac{1}{2e}$} | D. | [-e2,$\frac{1}{{e}^{2}}$)∪{$\frac{2}{3e}$} |
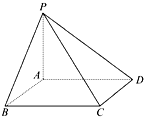 如图,ABCD为正方形,P为平面ABCD外一点,且PA⊥平面ABCD,则关于平面PAB、平面PBC、平面PAD的位置关系下列说法正确的有①④⑤
如图,ABCD为正方形,P为平面ABCD外一点,且PA⊥平面ABCD,则关于平面PAB、平面PBC、平面PAD的位置关系下列说法正确的有①④⑤