题目内容
已知函数f(x)=a•4x-2x+1+a+3.
(1)若a=0,解方程f(2x)=-5;
(2)若a=1,求f(x)的单调区间;
(3)若存在实数x0∈[-1,1],使f(x0)=4,求实数a的取值范围.
(1)若a=0,解方程f(2x)=-5;
(2)若a=1,求f(x)的单调区间;
(3)若存在实数x0∈[-1,1],使f(x0)=4,求实数a的取值范围.
(1)若a=0,由f(2x)=-5,即-22x+1+3=-5,
∴22x+1=8,∴22x+1=23,
∴2x+1=3
∴x=1(2分)
(2)若a=1,则f(x)=4x-2x+1+4,设x1,x2∈R,且x1<x2,
f(x2)-f(x1)=4x2-2x2+1+4-(4x1-2x1+1+4)=(4x2-4x1)-2(2x2-2x1)=(2x2-2x1)(2x2+2x1-2)
∵2x2-2x1>0
①当x1,x2∈[0,+∞)时,有2x2+2x1-2>0,
∴(2x2-2x1)(2x2+2x1-2)>0,
∴f(x2)>f(x1),
∴f(x)在[0,+∞)上是增函数;
②当x1,x2∈(-∞,0]时,有2x2+2x1-2<0,
∴(2x2-2x1)(2x2+2x1-2)<0,
∴f(x2)<f(x1),
∴f(x)在(-∞,0]上是减函数
∴f(x)的单调增区间是[0,+∞),单调减区间是(-∞,0](7分)
(3)设2x=t,由x0∈[-1,1],得t∈[
,2],且f(x)=a•4x-2x+1+a+3=a•t2-2t+a+3
∴存在t∈[
,2],使得a•t2-2t+a+3=4,即a•t2-2t+a-1=0
令g(t)=a•t2-2t+a-1,
若a=0,由f(x0)=4,无解.
若a≠0,则函数g(t)的对称轴是t=
由已知得方程g(t)=0在t∈[
,2]上有实数解
∴g(
)g(2)≤0或
∴(
a-2)(5a-5)≤0或
a≤
∴1≤a≤
或
≤a≤
∴实数a的取值范围为[1,
].
∴22x+1=8,∴22x+1=23,
∴2x+1=3
∴x=1(2分)
(2)若a=1,则f(x)=4x-2x+1+4,设x1,x2∈R,且x1<x2,
f(x2)-f(x1)=4x2-2x2+1+4-(4x1-2x1+1+4)=(4x2-4x1)-2(2x2-2x1)=(2x2-2x1)(2x2+2x1-2)
∵2x2-2x1>0
①当x1,x2∈[0,+∞)时,有2x2+2x1-2>0,
∴(2x2-2x1)(2x2+2x1-2)>0,
∴f(x2)>f(x1),
∴f(x)在[0,+∞)上是增函数;
②当x1,x2∈(-∞,0]时,有2x2+2x1-2<0,
∴(2x2-2x1)(2x2+2x1-2)<0,
∴f(x2)<f(x1),
∴f(x)在(-∞,0]上是减函数
∴f(x)的单调增区间是[0,+∞),单调减区间是(-∞,0](7分)
(3)设2x=t,由x0∈[-1,1],得t∈[
| 1 |
| 2 |
∴存在t∈[
| 1 |
| 2 |
令g(t)=a•t2-2t+a-1,
若a=0,由f(x0)=4,无解.
若a≠0,则函数g(t)的对称轴是t=
| 1 |
| a |
由已知得方程g(t)=0在t∈[
| 1 |
| 2 |
∴g(
| 1 |
| 2 |
|
∴(
| 5 |
| 4 |
|
1+
| ||
| 2 |
∴1≤a≤
| 8 |
| 5 |
| 8 |
| 5 |
1+
| ||
| 2 |
∴实数a的取值范围为[1,
1+
| ||
| 2 |

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
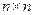 的矩
的矩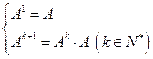 。若
。若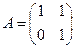 ,求(1)
,求(1)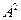 ,
,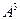 ;
;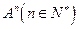 ,并用数学归纳法证明。
,并用数学归纳法证明。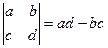 ,则不等式
,则不等式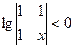 的解集是
的解集是