题目内容
(本题满分10分)已知二次函数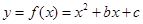 的图象过点(1,13),
的图象过点(1,13),
且函数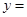
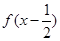 是偶函数.
是偶函数.
(1)求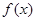 的解析式;
的解析式;
(2)已知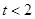 ,
,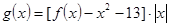 ,求函数
,求函数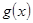 在[
在[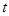 ,2]上的最大值和最小值.
,2]上的最大值和最小值.
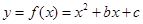 的图象过点(1,13),
的图象过点(1,13),且函数
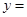
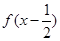 是偶函数.
是偶函数.(1)求
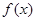 的解析式;
的解析式;(2)已知
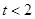 ,
,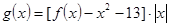 ,求函数
,求函数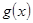 在[
在[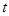 ,2]上的最大值和最小值.
,2]上的最大值和最小值.(1)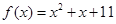 .
.
(2) =0.当
=0.当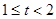 ,
,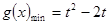 ;
;
当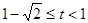 ,
,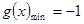 ;
;
当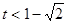 ,
,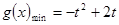 ;
;
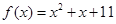 .
. (2)
 =0.当
=0.当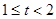 ,
,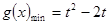 ;
;当
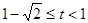 ,
,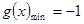 ;
;当
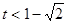 ,
,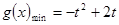 ;
; 本试题主要是考查了二次函数的解析式和二次函数性质的综合运用。
(1)因为函数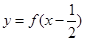 是偶函数,所以二次函数
是偶函数,所以二次函数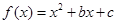 的对称轴方程为
的对称轴方程为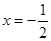 ,故
,故 .又因为二次函数
.又因为二次函数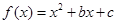 的图象过点(1,13),所以
的图象过点(1,13),所以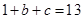 ,故
,故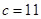 .得到解析式。
.得到解析式。
(2)因为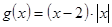 当
当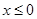 时,
时,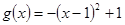 ,当
,当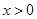 时,
时,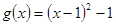 ,
,
得到 =0,同时可以得到最小值。
=0,同时可以得到最小值。
解 (1)因为函数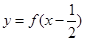 是偶函数,所以二次函数
是偶函数,所以二次函数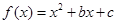 的对称轴方程为
的对称轴方程为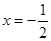 ,故
,故 . 又因为二次函数
. 又因为二次函数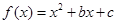 的图象过点(1,13),所以
的图象过点(1,13),所以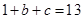 ,故
,故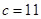 .因此,
.因此,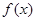 的解析式为
的解析式为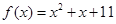 .
.
(2)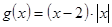 当
当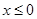 时,
时,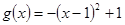 ,当
,当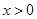 时,
时,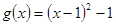 ,
,
由此可知 =0.当
=0.当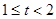 ,
,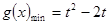 ;
;
当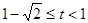 ,
,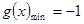 ;
;
当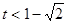 ,
,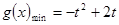 ;
;
(1)因为函数
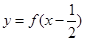 是偶函数,所以二次函数
是偶函数,所以二次函数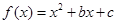 的对称轴方程为
的对称轴方程为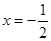 ,故
,故 .又因为二次函数
.又因为二次函数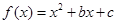 的图象过点(1,13),所以
的图象过点(1,13),所以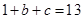 ,故
,故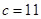 .得到解析式。
.得到解析式。(2)因为
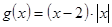 当
当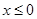 时,
时,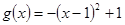 ,当
,当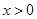 时,
时,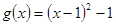 ,
,得到
 =0,同时可以得到最小值。
=0,同时可以得到最小值。解 (1)因为函数
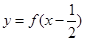 是偶函数,所以二次函数
是偶函数,所以二次函数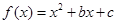 的对称轴方程为
的对称轴方程为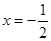 ,故
,故 . 又因为二次函数
. 又因为二次函数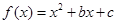 的图象过点(1,13),所以
的图象过点(1,13),所以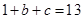 ,故
,故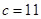 .因此,
.因此,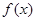 的解析式为
的解析式为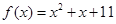 .
. (2)
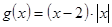 当
当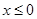 时,
时,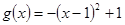 ,当
,当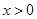 时,
时,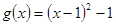 ,
,由此可知
 =0.当
=0.当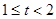 ,
,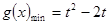 ;
;当
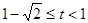 ,
,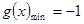 ;
;当
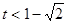 ,
,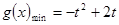 ;
; 
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

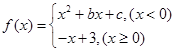 ,若
,若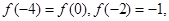

 的解析式;
的解析式; 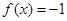 ,求相应
,求相应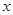 的值.
的值.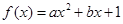 为定义在
为定义在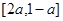 上的偶函数,则
上的偶函数,则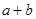 的值是( )
的值是( )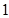
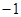
 或
或 或
或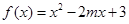 为
为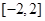 上的单调函数,则
上的单调函数,则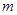 的取值范围为_________
的取值范围为_________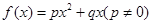 ,其导函数为
,其导函数为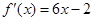 ,数列
,数列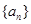 的前
的前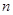 项和为
项和为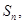 点
点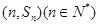 均在函数
均在函数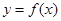 的图像上;.
的图像上;.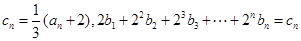 ,求数列
,求数列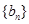 的通项公式;
的通项公式; 满足
满足 ,则
,则 .
. },则ab的值是 _____.
},则ab的值是 _____.