题目内容
14.已知双曲线$\frac{x^2}{2}-\frac{y^2}{m}=1$的一条准线与抛物线y2=4x的准线重合,则双曲线的离心率为$\sqrt{2}$.分析 先求得抛物线的准线方程,进而求得双曲线的准线方程表达式,进而求得b,则c可得,进而求得双曲线的离心率.
解答 解:依题意可知抛物线准线方程为x=-2,准线在x轴上
∴双曲线的准线方程为x=-$\frac{2}{\sqrt{2+m}}$,∴-$\frac{2}{\sqrt{2+m}}$=-1,解得m=2.
∴c=$\sqrt{2+m}$=2.
∴双曲线的离心率e=$\frac{c}{a}$=$\frac{2}{\sqrt{2}}$=$\sqrt{2}$.
故答案为:$\sqrt{2}$.
点评 本题主要考查了双曲线的简单性质.解题的关键是熟练掌握双曲线性质中长轴、短轴、焦距、离心率等之间的关系.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
4.如图,阅读程序框图,若输出的S的值等于55,那么在程序框图中的判断框内应填写的条件是( ) 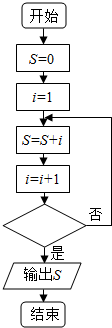

| A. | i>8 | B. | i>9 | C. | i>10 | D. | i>11 |
5.若函数y=cosx+ax在[-$\frac{π}{2}$,$\frac{π}{2}$]上是增函数,则实数a的取值范围是( )
| A. | (-∞,-1] | B. | (-∞,1] | C. | [-1,+∞) | D. | [1,+∞) |
19.如果测得(x,y)的四组数值分别是A(1,3),B(2,3.8),C(3,5.2),D(4,6),则y与x之间的线性回归方程为( )
| A. | $\widehat{y}$=1.04x+2 | B. | $\widehat{y}$=1.04x+1.9 | C. | $\widehat{y}$=1.05x+1.9 | D. | $\widehat{y}$=1.9x+1.04 |
6.已知平行六面体ABCD-A1B1C1D1,底面ABCD是边长为1的正方形,AA1=2,∠A1AB=∠A1AD=120°,则异面直线AC1与A1D所成角的余弦值为( )
| A. | $\frac{{\sqrt{6}}}{3}$ | B. | $\frac{{\sqrt{10}}}{5}$ | C. | $\frac{\sqrt{15}}{5}$ | D. | $\frac{{\sqrt{14}}}{7}$ |