题目内容
椭圆 (a>b>0)的两个焦点为F1、F2,短轴两端点B1、B2,已知F1、F2、B1、B2四点共圆,且点(0,3)到椭圆上的点的最远距离为
(a>b>0)的两个焦点为F1、F2,短轴两端点B1、B2,已知F1、F2、B1、B2四点共圆,且点(0,3)到椭圆上的点的最远距离为 ,则此椭圆的方程是
,则此椭圆的方程是
- A.
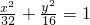
- B.
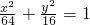
- C.
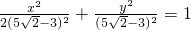
- D.
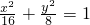
A
分析:由F1、F2、B1、B2四点共圆,得出b=c,进而得到a2=b2+c2=2b2,再设椭圆的方程(含参数b),设H(x,y)为椭圆上一点,化简点(0,3)到椭圆上的点的距离,利用其最大值,分类讨论求出参数b的值,即得椭圆的方程.
解答:∵F1、F2、B1、B2四点共圆,∴b=c,
∴a2=b2+c2=2b2,
设椭圆的方程为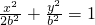 ,N(0,3),
,N(0,3),
设H(x,y)为椭圆上一点,则|HN|2=x2+(y-3)2=-(y+3)2+2b2+18,(-b≤y≤b),
①若0<b<3,|HN|2的最大值b2+6b+9=50得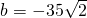 (舍去),
(舍去),
②若b≥3,|HN|2的最大值2b2+18=50得b2=16,
∴所求的椭圆的方程为: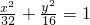 .
.
故选A.
点评:本题考查椭圆的性质及其应用、函数最值的求法等,解题时要注意分类讨论思想的合理运用.
分析:由F1、F2、B1、B2四点共圆,得出b=c,进而得到a2=b2+c2=2b2,再设椭圆的方程(含参数b),设H(x,y)为椭圆上一点,化简点(0,3)到椭圆上的点的距离,利用其最大值,分类讨论求出参数b的值,即得椭圆的方程.
解答:∵F1、F2、B1、B2四点共圆,∴b=c,
∴a2=b2+c2=2b2,
设椭圆的方程为
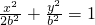 ,N(0,3),
,N(0,3),设H(x,y)为椭圆上一点,则|HN|2=x2+(y-3)2=-(y+3)2+2b2+18,(-b≤y≤b),
①若0<b<3,|HN|2的最大值b2+6b+9=50得
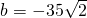 (舍去),
(舍去),②若b≥3,|HN|2的最大值2b2+18=50得b2=16,
∴所求的椭圆的方程为:
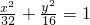 .
.故选A.
点评:本题考查椭圆的性质及其应用、函数最值的求法等,解题时要注意分类讨论思想的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (a>b>0)的离心率e=
(a>b>0)的离心率e= ,连接椭圆的四个顶点得到的菱形的面积为4.
,连接椭圆的四个顶点得到的菱形的面积为4.
 ,求直线l的倾斜角;
,求直线l的倾斜角; 在线段AB的垂直平分线上,且
在线段AB的垂直平分线上,且 .求
.求 的值.
的值. (a>b>0)的右焦点为F2(3,0),离心率为
(a>b>0)的右焦点为F2(3,0),离心率为 .
. (a>b>0)的焦距为4,且与椭圆
(a>b>0)的焦距为4,且与椭圆 有相同的离心率,斜率为k的直线l经过点M(0,1),与椭圆C交于不同两点A、B.
有相同的离心率,斜率为k的直线l经过点M(0,1),与椭圆C交于不同两点A、B. (a>b>0)的左,右焦点,若椭圆的右准线上存在一点P,使得线段PF1的垂直平分线过点F2,则离心率的范围是 .
(a>b>0)的左,右焦点,若椭圆的右准线上存在一点P,使得线段PF1的垂直平分线过点F2,则离心率的范围是 . 分)
分) (a>b>0)的离心率
(a>b>0)的离心率 ,焦距是函数
,焦距是函数 的零点.
的零点. 与椭圆交于
与椭圆交于 、
、 两点,
两点, ,求k的值.
,求k的值.