题目内容
【题目】已知定义域为![]() 的函数
的函数![]() 是奇函数.
是奇函数.
(1)求![]() 的值;
的值;
(2)判断函数![]() 的单调性并证明;
的单调性并证明;
(2)若关于![]() 的不等式
的不等式![]() 在
在![]() 有解,求实数
有解,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)见解析(3)
(2)见解析(3)![]()
【解析】试题分析:(1)由![]() 为奇函数可知,
为奇函数可知, ![]() ,即可得解;
,即可得解;
(2)由![]() 递增可知
递增可知![]() 在
在![]() 上为减函数,对于任意实数
上为减函数,对于任意实数![]() ,不妨设
,不妨设![]() ,化简
,化简![]() 判断正负即可证得;
判断正负即可证得;
(3)不等式![]() ,等价于
,等价于![]() ,即
,即![]() ,原问题转化为
,原问题转化为![]() 在
在![]() 上有解,求解
上有解,求解![]() 的最大值即可.
的最大值即可.
试题解析
解:(1)由![]() 为奇函数可知,
为奇函数可知, ![]() ,解得
,解得![]() .
.
(2)由![]() 递增可知
递增可知![]() 在
在![]() 上为减函数,
上为减函数,
证明:对于任意实数![]() ,不妨设
,不妨设![]() ,
,
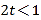
∵![]() 递增,且
递增,且![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() ,故
,故![]() 在
在![]() 上为减函数.
上为减函数.
(3)关于![]() 的不等式
的不等式![]() ,
,
等价于![]() ,即
,即![]() ,
,
因为![]() ,所以
,所以![]() ,
,
原问题转化为![]() 在
在![]() 上有解,
上有解,
∵![]() 在区间
在区间![]() 上为减函数,
上为减函数,
∴![]() ,
, ![]() 的值域为
的值域为![]() ,
,
∴![]() ,解得
,解得![]() ,
,
∴![]() 的取值范围是
的取值范围是![]() .
.
点晴:本题属于对函数单调性应用的考察,若函数![]() 在区间上单调递增,则
在区间上单调递增,则![]() 时,有
时,有![]() ,事实上,若
,事实上,若![]() ,则
,则![]() ,这与
,这与![]() 矛盾,类似地,若
矛盾,类似地,若![]() 在区间上单调递减,则当
在区间上单调递减,则当![]() 时有
时有![]() ;据此可以解不等式,由函数值的大小,根据单调性就可以得自变量的大小关系.本题中可以利用对称性数形结合即可.
;据此可以解不等式,由函数值的大小,根据单调性就可以得自变量的大小关系.本题中可以利用对称性数形结合即可.

【题目】某市对大学生毕业后自主创业人员给予小额贷款补贴,贷款期限分为6个月、12个月、18个月、24个月、36个月五种,对于这五种期限的贷款政府分别补贴200元、300元、300元、400元、400元,从2016年享受此项政策的自主创业人员中抽取了100人进行调查统计,选取贷款期限的频数如表:
贷款期限 | 6个月 | 12个月 | 18个月 | 24个月 | 36个月 |
频数 | 20 | 40 | 20 | 10 | 10 |
以上表中各种贷款期限的频数作为2017年自主创业人员选择各种贷款期限的概率.
(Ⅰ)某大学2017年毕业生中共有3人准备申报此项贷款,计算其中恰有两人选择贷款期限为12个月的概率;
(Ⅱ)设给某享受此项政策的自主创业人员补贴为X元,写出X的分布列;该市政府要做预算,若预计2017年全市有600人申报此项贷款,则估计2017年该市共要补贴多少万元.