题目内容
现有流量均为300m3/s的两条河流A,B汇合于某处后,不断混合,它们的含沙量分别为2kg/m3和0.2kg/m3.假设从汇合处开始,沿岸设有若干个观测点,两股水流在流往相邻两个观测点的过程中,其混合效果相当于两股水流在1秒内交换100m3的水量,其交换过程为从A股流入B股100m3的水量,经混合后,又从B股流入A股100m3水并混合,问从第几个观测点开始,两股河水的含沙量之差小于0.01kg/m3.(不考虑泥沙沉淀).
分析:我们设第n个观测点A股水流含沙量为an,B股水流含沙量为bn.由已知我们易得{an-bn}是以a1-b1为首项,
为公比的等比数列.求出数列的通项公式后,构造不等式,解不不等式,即可得到结论.
| 1 |
| 2 |
解答:解:设第n个观测点A股水流含沙量为ankg/m3,B股水流含沙量为bn.
an=
(200an+100bn)=
(3an-1+bn-1)
即:an-bn=
(an-1-bn-1)
∴{an-bn}是以a1-b1为首项,
为公比的等比数列.
an-bn=1.8•(
)n-1
解不等式1.8•(
)n-1<10-2
得2n-1>180,又由n正整数,
∴n≥9
因此,从第9个观测点开始,两股水流含沙量之差小于0.01kg/m3.
an=
| 1 |
| 300 |
| 1 |
| 4 |
即:an-bn=
| 1 |
| 2 |
∴{an-bn}是以a1-b1为首项,
| 1 |
| 2 |
an-bn=1.8•(
| 1 |
| 2 |
解不等式1.8•(
| 1 |
| 2 |
得2n-1>180,又由n正整数,
∴n≥9
因此,从第9个观测点开始,两股水流含沙量之差小于0.01kg/m3.
点评:本题考查等比数列的概念,不等式的解法,及应用数学知识解决实际问题的能力.在求数列的通项公式过程中,我们要分析数列项与项之间的关系,尽可能将数列转化为特殊数列(等差、等比),在解不等式时,我们要结合指数函数的性质,并结合n的实际意义进行解答.

练习册系列答案
相关题目
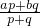 kg/m3
kg/m3