题目内容
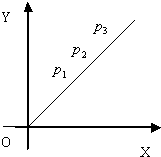 如图,在正比例函数y=kx(k>0)图象上有一列点P1,P2,P3,P4,…,Pn,….已知n≥2时,
如图,在正比例函数y=kx(k>0)图象上有一列点P1,P2,P3,P4,…,Pn,….已知n≥2时,| Pn-1Pn+1 |
Pn
|
(1)求出a2,a3的值;
(2)求数列{an}的通项公式;
(3)设点Mn(n,an)(n≥2,n∈N),证明:这些点中不可能同时有两个点在正比例函数y=kx(k>0)的图象上.
分析:(1)由题设条件结合向量和的运算,知|
|=(n-1)|
|,从而得出数列{an}的递推关系式,即可得出a2,a3的值;
(2)将(1)中的a1=(2-1)a2,a2=(3-1)a3,a3=(4-1)a4.…,an=nan+1等关系式相乘即可得数列{an}的通项公式;
(3)对于结论是否定形式的命题,往往反证法证明.
| Pn-1Pn |
Pn
|
(2)将(1)中的a1=(2-1)a2,a2=(3-1)a3,a3=(4-1)a4.…,an=nan+1等关系式相乘即可得数列{an}的通项公式;
(3)对于结论是否定形式的命题,往往反证法证明.
解答:解:(1)由
=n
得
+
=n
,
∴
=(n-1)
∴|
|=(n-1)|
|,
即a1=(2-1)a2,a2=(3-1)a3,a3=(4-1)a4.…,an=nan+1
∴a2=1,a3=
(2)将(1)中的a1=(2-1)a2,a2=(3-1)a3,a3=(4-1)a4.…,
an=nan+1等关系式相乘得a1=1•2•3•4•…•n•an+1,
即an+1=
∴an=
(3)设点Mm(m,am),Nn(n,an)(m≠n)在正比例函数y=kx(k>0),
则am=km,an=kn,即km=
,kn=
∴k=
,k=
,从而1•2•3•…•m=1•2•3•…•n
这与m≠n矛盾,故不可能同时有两个点在正比例函数y=kx(k>0)的图象上.
| Pn-1Pn+1 |
Pn
|
| Pn-1Pn |
| PnPn+1 |
Pn
|
∴
| Pn-1Pn |
Pn
|
| Pn-1Pn |
Pn
|
即a1=(2-1)a2,a2=(3-1)a3,a3=(4-1)a4.…,an=nan+1
∴a2=1,a3=
| 1 |
| 2 |
(2)将(1)中的a1=(2-1)a2,a2=(3-1)a3,a3=(4-1)a4.…,
an=nan+1等关系式相乘得a1=1•2•3•4•…•n•an+1,
即an+1=
| 1 |
| 1•2•3•…•n |
| 1 |
| 1•2•3•…•(n-1) |
(3)设点Mm(m,am),Nn(n,an)(m≠n)在正比例函数y=kx(k>0),
则am=km,an=kn,即km=
| 1 |
| 1•2•3•…•(m-1) |
| 1 |
| 1•2•3•…•(n-1) |
∴k=
| 1 |
| 1•2•3•…•m |
| 1 |
| 1•2•3•…•n |
这与m≠n矛盾,故不可能同时有两个点在正比例函数y=kx(k>0)的图象上.
点评:本题考查数列现解析几何的综合运用,解题时要认真审题,注意挖掘题设中的隐含条件,合理地应用反证法.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
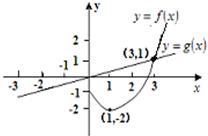 对于任意的实数a,b,记max{a,b}=
对于任意的实数a,b,记max{a,b}=
|
| A、y=F(x)为奇函数 |
| B、y=F(x)在(-3,0)上为增函数 |
| C、y=F(x)的最小值为-2,最大值为2 |
| D、以上说法都不正确 |
 对于任意的实数a、b,记max{a,b}=
对于任意的实数a、b,记max{a,b}=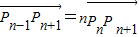 .设线段P1P2,P2P3,P3P4,…,PnPn+1的长分别为a1,a2,a3,…,an,且a1=1.
.设线段P1P2,P2P3,P3P4,…,PnPn+1的长分别为a1,a2,a3,…,an,且a1=1.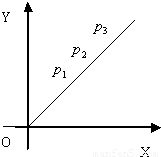
 的图像相交于点A(a,2),将直线l1向上平移3个单位得到的直线l2与双曲线相交于B、C两点(点B在第一象限),与y轴交于点D.
的图像相交于点A(a,2),将直线l1向上平移3个单位得到的直线l2与双曲线相交于B、C两点(点B在第一象限),与y轴交于点D.