题目内容
如图,在直角△ABC中,∠C=90°,AB=2BC,E、F为线段AC、AB上的点,EF∥BC,将△AEF沿直线EF翻折成△A'EF,使平面A'EF⊥平面BCE,且T为A'B中点,FT∥平面△A'EC
(1)问E点在什么位置?并说明理由;
(2)求直线FC与平面A'BC所成角的正弦值.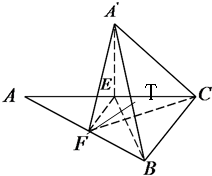
(1)问E点在什么位置?并说明理由;
(2)求直线FC与平面A'BC所成角的正弦值.

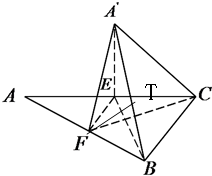
(1)由已知得T为A'B的中点,取A'C的中点记为S,连接ES、TS,易得EF∥ST,
由平面EFTS∩平面A'EC=ES,FT∥平面A'EC,得FT∥ES,
四边形EFTS为平行四边形,得EF=ST,而ST=
| 1 |
| 2 |
所以E为AC中点.
(2)E为中点,即A'E=EC,则ES⊥A'C,易得BC⊥面A'EC,所以ES⊥面A'BC; ES
| ||
| . |
sin∠FCT=
| FT |
| FC |
| ||||||||
| 1 |
| ||
| 4 |

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
 如图,在直角△ABC中,∠C=90°,AB=2BC,E、F为线段AC、AB上的点,EF∥BC,将△AEF沿直线EF翻折成△A'EF,使平面A'EF⊥平面BCE,且T为A'B中点,FT∥平面△A'EC
如图,在直角△ABC中,∠C=90°,AB=2BC,E、F为线段AC、AB上的点,EF∥BC,将△AEF沿直线EF翻折成△A'EF,使平面A'EF⊥平面BCE,且T为A'B中点,FT∥平面△A'EC 如图,在直角△ABC中,AB=AC=2,分别以A,B,C为圆心,以
如图,在直角△ABC中,AB=AC=2,分别以A,B,C为圆心,以