题目内容
 如图,在直角△ABC中,AB=AC=2,分别以A,B,C为圆心,以
如图,在直角△ABC中,AB=AC=2,分别以A,B,C为圆心,以| 1 |
| 2 |
2-
| π |
| 2 |
2-
.| π |
| 2 |
分析:阴影部分的面积是三角形ABC的面积减去三个扇形的面积,就是一个半圆的面积,然后根据扇形的面积公式和三角形的面积公式计算即可.
解答: 解:因为AB=AC=2,三角形是等腰直角三角形,
解:因为AB=AC=2,三角形是等腰直角三角形,
并且A+B+C=π,所以三个扇形的面积就是一个半圆的面积,即S=
•π•(
AC2)=
,
∴S阴影部分=S△ABC-S=
•2•2-
=2-
.
故答案为:2-
.
 解:因为AB=AC=2,三角形是等腰直角三角形,
解:因为AB=AC=2,三角形是等腰直角三角形,并且A+B+C=π,所以三个扇形的面积就是一个半圆的面积,即S=
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 2 |
∴S阴影部分=S△ABC-S=
| 1 |
| 2 |
| π |
| 2 |
| π |
| 2 |
故答案为:2-
| π |
| 2 |
点评:本题考查了扇形的面积公式以及三角形的面积公式,基本知识的考查.

练习册系列答案
相关题目
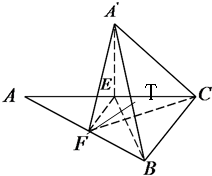
 如图,在直角△ABC中,∠C=90°,AB=2BC,E、F为线段AC、AB上的点,EF∥BC,将△AEF沿直线EF翻折成△A'EF,使平面A'EF⊥平面BCE,且T为A'B中点,FT∥平面△A'EC
如图,在直角△ABC中,∠C=90°,AB=2BC,E、F为线段AC、AB上的点,EF∥BC,将△AEF沿直线EF翻折成△A'EF,使平面A'EF⊥平面BCE,且T为A'B中点,FT∥平面△A'EC