题目内容
 选做题(请考生在三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)
选做题(请考生在三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)(A)(坐标系与参数方程选做题)在直角坐标系x0y中,以原点为极点,x轴非负半轴为极轴建立极坐标系,已知圆C与直线l的方程分别为:
 (t为参数).若圆C被直线l平分,则实数x的值为 .
(t为参数).若圆C被直线l平分,则实数x的值为 .(B)(不等式选做题)若关于x的不等式|x-m|<2成立的充分不必要条件是2≤x≤3,则实数m的取值范围是 .
(C) (几何证明选讲) 如图,割线PBC经过圆心O,OB=PB=1,OB绕点O逆时针旋转120°到OD,连PD交圆O于点E,则PE= .
【答案】分析:A.若圆C被直线l平分,只需直线经过圆的圆心.化圆、直线方程为普通方程,求出圆心坐标,代入直线方程求解.
B.首先分析题目已知不等式|x-m|<1成立的充分不必要条件是2≤x≤3,求m的取值范围,故可以考虑先根据绝对值不等式的解法解出|x-m|<1含有参数m的解,又因为充分不必要条件,是条件可以推出结论,结论推不出条件,即2≤x≤3是|x-m|<1解集的子集.先由余弦定理求出PD,再根据割线定理即可求出PE,问题解决.
C.先由余弦定理求出PD,再根据割线定理即可求出PE,问题解决.
解答:解:A.圆的极坐标方程为:ρ=2sinθ,即:ρ2=2ρsinθ,
化为直角坐标方程为x2+y2=2y,即为x2+(y-1)2=1.
表示以C(0,1)为圆心,半径为1 的圆.
线l的方程化为x-x=y,
若圆C被直线l平分,只需直线经过圆的圆心,所以x=-1
故答案为:-1
B.因为|x-m|<2,即-2<x-m<2,即m-2<x<m+2;
由已知不等式|x-m|<1成立的充分非必要条件是2≤x≤3
即2≤x≤3是|x-m|<1解集的子集,即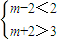
解得实数m的取值范围是(1,4)
C.由余弦定理得,PD2=OD2+OP2-2OD•OPcos120°=1+4-2×1×2×(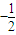 )=7,所以PD=
)=7,所以PD=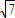 .
.
根据割线定理PE•PD=PB•PC得,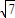 PE=1×3,PE=
PE=1×3,PE=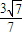
故答案为: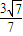
点评:A.本题以曲线参数方程出发,考查了极坐标方程、普通方程间的互化,直线和圆的位置关系.
B.主要考查绝对值不等式的解法问题,其中涉及到必要条件、充分条件的知识,题目的计算量小,主要考查的是概念性问题,属于基础题目.
C已知三角形两边与夹角时,一定要想到余弦定理的运用,之后做题的思路也许会豁然开朗.
B.首先分析题目已知不等式|x-m|<1成立的充分不必要条件是2≤x≤3,求m的取值范围,故可以考虑先根据绝对值不等式的解法解出|x-m|<1含有参数m的解,又因为充分不必要条件,是条件可以推出结论,结论推不出条件,即2≤x≤3是|x-m|<1解集的子集.先由余弦定理求出PD,再根据割线定理即可求出PE,问题解决.
C.先由余弦定理求出PD,再根据割线定理即可求出PE,问题解决.
解答:解:A.圆的极坐标方程为:ρ=2sinθ,即:ρ2=2ρsinθ,
化为直角坐标方程为x2+y2=2y,即为x2+(y-1)2=1.
表示以C(0,1)为圆心,半径为1 的圆.
线l的方程化为x-x=y,
若圆C被直线l平分,只需直线经过圆的圆心,所以x=-1
故答案为:-1
B.因为|x-m|<2,即-2<x-m<2,即m-2<x<m+2;
由已知不等式|x-m|<1成立的充分非必要条件是2≤x≤3
即2≤x≤3是|x-m|<1解集的子集,即
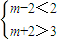
解得实数m的取值范围是(1,4)
C.由余弦定理得,PD2=OD2+OP2-2OD•OPcos120°=1+4-2×1×2×(
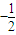 )=7,所以PD=
)=7,所以PD=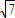 .
.根据割线定理PE•PD=PB•PC得,
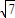 PE=1×3,PE=
PE=1×3,PE=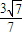
故答案为:
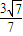
点评:A.本题以曲线参数方程出发,考查了极坐标方程、普通方程间的互化,直线和圆的位置关系.
B.主要考查绝对值不等式的解法问题,其中涉及到必要条件、充分条件的知识,题目的计算量小,主要考查的是概念性问题,属于基础题目.
C已知三角形两边与夹角时,一定要想到余弦定理的运用,之后做题的思路也许会豁然开朗.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
 选做题(请考生在三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)
选做题(请考生在三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分) 选做题(请考生在三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分).
选做题(请考生在三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分). 的圆心,且垂直于极轴的直线的极坐标
的圆心,且垂直于极轴的直线的极坐标 方程为 。
方程为 。 的不等式
的不等式 是常数)的解是非空集合,则
是常数)的解是非空集合,则 的取
的取 值范围 。
值范围 。 ,
, ,
, 与
与 交于点D,且
交于点D,且 ,
, ,则
,则 。
。 
