题目内容
 选做题(请考生在三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分).
选做题(请考生在三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分).(A)(坐标系与参数方程) 在极坐标系中,过圆ρ=6cosθ的圆心,且垂直于极轴的直线的极坐标方程为
ρcosθ=3
ρcosθ=3
.(B)(不等式选讲)已知关于x的不等式|x+a|+|x-1|+a<2011(a是常数)的解是非空集合,则a的取值范围
a<1005
a<1005
.(C)(几何证明选讲)如图:若PA=PB,∠APB=2∠ACB,AC与PB交于点D,且PB=4,PD=3,则AD•DC=
7
7
.分析:(A) 把圆的极坐标方程化为普通方程,求出圆心和直线方程,再把它化成极坐标方程.
(B)|x+a|+|x-1|表示数轴上的x到-a和1的距离之和,其最小值为|1+a|,故有|1+a|<2011-a,从而求出a的取值范围.
(C)以P为圆心,以PA=PB为半径作圆,延长BD交圆于M,如图,证明C在圆上,利用AD•DC=BD•DM来求出它的值.
(B)|x+a|+|x-1|表示数轴上的x到-a和1的距离之和,其最小值为|1+a|,故有|1+a|<2011-a,从而求出a的取值范围.
(C)以P为圆心,以PA=PB为半径作圆,延长BD交圆于M,如图,证明C在圆上,利用AD•DC=BD•DM来求出它的值.
解答: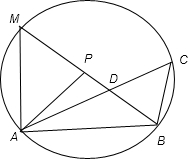 解:(A)圆ρ=6cosθ 即 ρ2=6ρcosθ,(x-3)2+y2=9,表示圆心在(3,0),半径等于3的圆.
解:(A)圆ρ=6cosθ 即 ρ2=6ρcosθ,(x-3)2+y2=9,表示圆心在(3,0),半径等于3的圆.
过圆心且垂直于极轴的直线为 x=3,即 ρ cosθ=3,故答案为 ρ cosθ=3.
(B)|x+a|+|x-1|表示数轴上的x到-a和1的距离之和,其最小值为|1+a|,
不等式即|x+a|+|x-1|<2011-a,∴|1+a|<2011-a,
∴a-2011<1+a<2011-a,∴a<1005,故 答案为 a<1005.
(C)以P为圆心,以PA=PB为半径作圆,延长BD交圆于M,如图:PA=PB=4,∠APB=2∠ACB,AC与PB交于点D,PD=3,
设∠ACB=θ,则∠APM=2θ,又∠ACB=θ,∴C在圆上.
∴AD•DC=BD•DM=BD•(PM+PD)=1•(4+3)=7,
故答案为 7.
 解:(A)圆ρ=6cosθ 即 ρ2=6ρcosθ,(x-3)2+y2=9,表示圆心在(3,0),半径等于3的圆.
解:(A)圆ρ=6cosθ 即 ρ2=6ρcosθ,(x-3)2+y2=9,表示圆心在(3,0),半径等于3的圆.过圆心且垂直于极轴的直线为 x=3,即 ρ cosθ=3,故答案为 ρ cosθ=3.
(B)|x+a|+|x-1|表示数轴上的x到-a和1的距离之和,其最小值为|1+a|,
不等式即|x+a|+|x-1|<2011-a,∴|1+a|<2011-a,
∴a-2011<1+a<2011-a,∴a<1005,故 答案为 a<1005.
(C)以P为圆心,以PA=PB为半径作圆,延长BD交圆于M,如图:PA=PB=4,∠APB=2∠ACB,AC与PB交于点D,PD=3,
设∠ACB=θ,则∠APM=2θ,又∠ACB=θ,∴C在圆上.
∴AD•DC=BD•DM=BD•(PM+PD)=1•(4+3)=7,
故答案为 7.
点评:本题考查极坐标方程与普通方程的互化,绝对值不等式的解法,体现了数形结合的数学思想.

练习册系列答案
相关题目
 选做题(请考生在三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)
选做题(请考生在三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分) 的圆心,且垂直于极轴的直线的极坐标
的圆心,且垂直于极轴的直线的极坐标 方程为 。
方程为 。 的不等式
的不等式 是常数)的解是非空集合,则
是常数)的解是非空集合,则 的取
的取 值范围 。
值范围 。 ,
, ,
, 与
与 交于点D,且
交于点D,且 ,
, ,则
,则 。
。 
 选做题(请考生在三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)
选做题(请考生在三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分) (t为参数).若圆C被直线l平分,则实数x的值为 .
(t为参数).若圆C被直线l平分,则实数x的值为 .