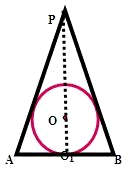
题目内容
若一个球的外切圆锥的高是这个球的直径的两倍,求圆锥的全面积与球的表面积之比.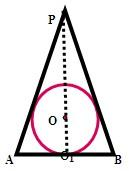
分析:设出球的半径,利用三角形相似,求出圆锥的底面半径,然后求出球的表面积,圆锥的全面积,即可得到比值.
解答: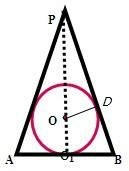 解:设球的半径为:1;圆锥的高为:4
解:设球的半径为:1;圆锥的高为:4
则圆锥的底面半径为:r
由△POD∽△PO1B
=
即
=
所以r=
圆锥的全面积为:2π+
×3
×2
π=8π
球的表面积为:4π
所以圆锥的全面积与球的表面积之比:2.
 解:设球的半径为:1;圆锥的高为:4
解:设球的半径为:1;圆锥的高为:4则圆锥的底面半径为:r
由△POD∽△PO1B
| OD |
| O1B |
| PO |
| O1P |
2
| ||
| 4 |
| 1 |
| r |
所以r=
| 2 |
圆锥的全面积为:2π+
| 1 |
| 2 |
| 2 |
| 2 |
球的表面积为:4π
所以圆锥的全面积与球的表面积之比:2.
点评:本题考查圆锥的内接球,考查二者的表面积,画出图形,找出二者的关系是解题的关键,利用相似是中学数学解题的一个特色,本题考查计算能力,是基础题.

练习册系列答案
相关题目
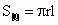 ).
). ).
).