题目内容
已知曲线y= x3+
x3+ ,
,
(1)求曲线过点P(2,4)的切线方程.
(2)求曲线的斜率为4的切线方程.
 x3+
x3+ ,
,(1)求曲线过点P(2,4)的切线方程.
(2)求曲线的斜率为4的切线方程.
(1) 4x-y-4=0或x-y+2=0 (2) 4x-y-4=0和12x-3y+20=0
(1)设曲线y= x3+
x3+ 与过点P(2,4)的切线相切于点A(x0,
与过点P(2,4)的切线相切于点A(x0,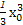 +
+ ),则点A处切线的斜率k=
),则点A处切线的斜率k=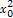 ,∴切线方程为y-(
,∴切线方程为y-(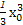 +
+ )=
)=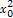 (x-x0),即y=
(x-x0),即y=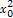 ·x-
·x-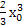 +
+ .
.
∵点P(2,4)在切线上,∴4=2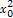 -
-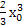 +
+ ,即
,即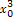 -3
-3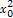 +4=0,∴
+4=0,∴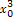 +
+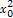 -4
-4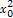 +4=0,
+4=0,
∴(x0+1)(x0-2)2=0,
解得x0=-1或x0=2,
故所求切线的方程为4x-y-4=0或x-y+2=0.
(2)设切点为(x0,y0),
则切线的斜率为k=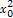 =4,x0=±2,
=4,x0=±2,
所以切点为(2,4),(-2,- ),
),
∴切线方程为y-4=4(x-2)和y+ =4(x+2),
=4(x+2),
即4x-y-4=0和12x-3y+20=0.
 x3+
x3+ 与过点P(2,4)的切线相切于点A(x0,
与过点P(2,4)的切线相切于点A(x0,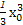 +
+ ),则点A处切线的斜率k=
),则点A处切线的斜率k=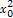 ,∴切线方程为y-(
,∴切线方程为y-(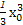 +
+ )=
)=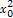 (x-x0),即y=
(x-x0),即y=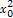 ·x-
·x-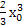 +
+ .
.∵点P(2,4)在切线上,∴4=2
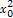 -
-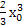 +
+ ,即
,即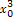 -3
-3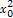 +4=0,∴
+4=0,∴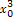 +
+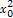 -4
-4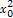 +4=0,
+4=0,∴(x0+1)(x0-2)2=0,
解得x0=-1或x0=2,
故所求切线的方程为4x-y-4=0或x-y+2=0.
(2)设切点为(x0,y0),
则切线的斜率为k=
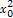 =4,x0=±2,
=4,x0=±2,所以切点为(2,4),(-2,-
 ),
),∴切线方程为y-4=4(x-2)和y+
 =4(x+2),
=4(x+2),即4x-y-4=0和12x-3y+20=0.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
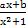 在点(-1,f(-1))处的切线方程为x+y+3=0.
在点(-1,f(-1))处的切线方程为x+y+3=0.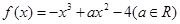 .
.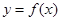 的图像在点
的图像在点 处的切线的倾斜角为
处的切线的倾斜角为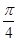 ,求
,求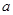 的值;
的值;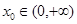 使
使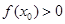 ,求
,求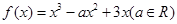 .
.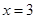 是
是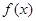 的极值点,求
的极值点,求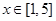 上的最大值;
上的最大值;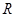 上的单调递增函数,求实数
上的单调递增函数,求实数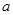 的取值范围.
的取值范围.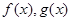 都是定义在R上的函数,
都是定义在R上的函数,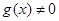 ,
,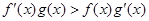 ,且
,且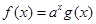
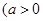 ,且
,且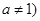 ,
,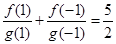 .若数列
.若数列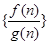 的前n项和大于62,则n的最小值为( )
的前n项和大于62,则n的最小值为( )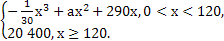


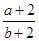 的取值范围是( )
的取值范围是( )