题目内容
若圆(x-a)2+(y-b)2=b2+1始终平分圆(x+1)2+(y+1)2=4的周长,则a、b应满足的关系式是( )
A.a2-2a-2b-3=0
B.a2+2a+2b+5=0
C.a2+2b2+2a+2b+1=0
D.3a2+2b2+2a+2b+1=0
B
[解析] 利用公共弦始终经过圆(x+1)2+(y+1)2=4的圆心即可求得.两圆的公共弦所在直线方程为:(2a+2)x+(2b+2)y-a2-1=0,它过圆心(-1,-1),代入得a2+2a+2b+5=0.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
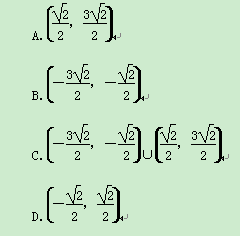
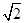 ,则实数a的值为
,则实数a的值为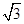 B.1或3 C.-2或6 D.0或4
B.1或3 C.-2或6 D.0或4