题目内容

若圆(x－a)2＋(y－b)2＝b2＋1始终平分圆(x＋1)2＋(y＋1)2＝4的周长，则a、b应满足的关系式是

[　　]

A．a2－2a－2b－3＝0

B．a2＋2a＋2b＋5＝0

C．a2＋2b2＋2a＋2b＋1＝0

D．3a2＋2b2＋2a＋2b＋1＝0

答案：B
解析：

利用两圆的公共弦始终经过圆(x＋1)2＋(y＋1)2＝4的圆心即可求得．把两圆分别化成一般式方程，作差可得公共弦方程为(2a＋2)x＋(2b＋2)y－a2－1＝0，它经过圆心(－1，－1)，代入后有a2＋2a＋2b＋5＝0．


练习册系列答案
相关题目

若直线x－y＋1＝0与圆(x－a)2＋y2＝2有公共点，则实数a取值范围是(　　)

A．[－3，－1]                           B．[－1,3]

C．[－3,1]                              D．(－∞，－3]∪[1，＋∞)

若圆(x－a)2＋(y－b)2＝b2＋1始终平分圆(x＋1)2＋(y＋1)2＝4的周长，则a、b应满足的关系式是(　　)

A．a2－2a－2b－3＝0

B．a2＋2a＋2b＋5＝0

C．a2＋2b2＋2a＋2b＋1＝0

D．3a2＋2b2＋2a＋2b＋1＝0

(2011～2012·湖南长沙模拟)若圆(x－a)2＋(y－a)2＝4上，总存在不同的两点到原点的距离等于1，则实数a的取值范围是(　　)

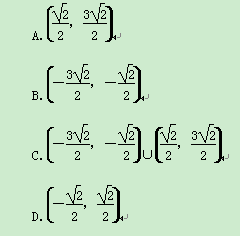
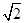若直线x－y＝2被圆(x－a)2＋y2＝4所截得的弦长为2，则实数a的值为

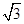A．－1或        B．1或3            C．－2或6          D．0或4

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网