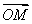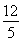题目内容
已知圆心(a，b)(a<0，b<0)在直线y＝2x＋1上的圆，其圆心到x轴的距离恰好等于圆的半径，在y轴上截得的弦长为2
，则圆的方程为( )
A．(x＋2)2＋(y＋3)2＝9 B．(x＋3)2＋(y＋5)2＝25
C．(x＋6)2＋
2＝
D.
2＋
2＝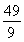
A
【解析】由圆心到x轴的距离恰好等于圆的半径知，所求圆与x轴相切，由题意得圆的半径为|b|，则圆的方程为(x－a)2＋(y－b)2＝b2.由于圆心在直线y＝2x＋1上，得b＝2a＋1 ①，令x＝0，得(y－b)2＝b2－a2，此时在y轴上截得的弦长为|y1－y2|＝2 
，由已知得，2 
＝2
，即b2－a2＝5 ②，由①②得
或
(舍去)．所以，所求圆的方程为(x＋2)2＋(y＋3)2＝9.故选A.
练习册系列答案
夺冠训练单元期末冲刺100分系列答案
相关题目
