题目内容
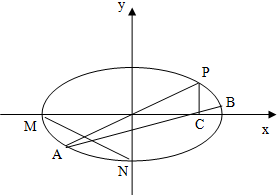 如图,在平面直角坐标系xOy中,M、N分别是椭圆
如图,在平面直角坐标系xOy中,M、N分别是椭圆| x2 |
| 4 |
| y2 |
| 2 |
(1)若直线PA平分线段MN,求k的值;
(2)当k=2时,求点P到直线AB的距离d;
(3)对任意k>0,求证:PA⊥PB.
分析:(1)由题设写出点M,N的坐标,求出线段MN中点坐标,根据线PA过原点和斜率公式,即可求出k的值;
(2)写出直线PA的方程,代入椭圆,求出点P,A的坐标,求出直线AB的方程,根据点到直线的距离公式,即可求得点P到直线AB的距离d;
(3)要证PA⊥PB,只需证直线PB与直线PA的斜率之积为-1,根据题意求出它们的斜率,即证的结果.
(2)写出直线PA的方程,代入椭圆,求出点P,A的坐标,求出直线AB的方程,根据点到直线的距离公式,即可求得点P到直线AB的距离d;
(3)要证PA⊥PB,只需证直线PB与直线PA的斜率之积为-1,根据题意求出它们的斜率,即证的结果.
解答:解:(1)由题设知,a=2,b=
,
故M(-2,0),N(0,-
),所以线段MN中点坐标为(-1,-
).
由于直线PA平分线段MN,故直线PA过线段MN的中点,又直线PA过原点,
所以k=
.
(2)直线PA的方程为y=2x,代入椭圆方程得
+
=1,解得x=±
,
因此P(
,
),A(-
,-
)
于是C(
,0),直线AC的斜率为1,故直线AB的方程为x-y-
=0.
因此,d=
=
.
(3)设P(x1,y1),B(x2,y2),则x1>0,x2>0,x1≠x2,
A(-x1,-y1),C(x1,0).
设直线PB,AB的斜率分别为k1,k2.
因为C在直线AB上,所以k2=
=
=
,
从而kk1+1=2k1k2+1=2•
•
+1=
+1
=
=
=0.
因此kk1=-1,所以PA⊥PB.
| 2 |
故M(-2,0),N(0,-
| 2 |
| ||
| 2 |
由于直线PA平分线段MN,故直线PA过线段MN的中点,又直线PA过原点,
所以k=
| ||
| 2 |
(2)直线PA的方程为y=2x,代入椭圆方程得
| x2 |
| 4 |
| 4x2 |
| 2 |
| 2 |
| 3 |
因此P(
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
于是C(
| 2 |
| 3 |
| 2 |
| 3 |
因此,d=
|
| ||||||
|
2
| ||
| 3 |
(3)设P(x1,y1),B(x2,y2),则x1>0,x2>0,x1≠x2,
A(-x1,-y1),C(x1,0).
设直线PB,AB的斜率分别为k1,k2.
因为C在直线AB上,所以k2=
| 0-(-y1) |
| x1-(-x1) |
| y1 |
| 2x1 |
| k |
| 2 |
从而kk1+1=2k1k2+1=2•
| y2-y1 |
| x2- x1 |
| y2-(-y1) |
| x2-(-x1) |
2
| ||||
|
=
| ||||||||
|
| 4-4 |
| x22-x12 |
因此kk1=-1,所以PA⊥PB.
点评:此题是个难题.考查椭圆的标准方程和简单的几何性质,以及直线斜率的求法,以及直线与椭圆的位置关系,体现了方程的思想和数形结合思想,同时也考查了学生观察、推理以及创造性地分析问题、解决问题的能力.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
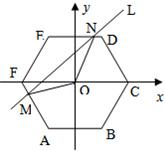 如图,在直角坐标平面内有一个边长为a、中心在原点O的正六边形ABCDEF,AB∥Ox.直线L:y=kx+t(k为常数)与正六边形交于M、N两点,记△OMN的面积为S,则函数S=f(t)的奇偶性为( )
如图,在直角坐标平面内有一个边长为a、中心在原点O的正六边形ABCDEF,AB∥Ox.直线L:y=kx+t(k为常数)与正六边形交于M、N两点,记△OMN的面积为S,则函数S=f(t)的奇偶性为( )| A、偶函数 | B、奇函数 | C、不是奇函数,也不是偶函数 | D、奇偶性与k有关 |
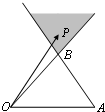 如图,在△OAB中,点P是线段OB及线段AB延长线所围成的阴影区域(含边界)的任意一点,且
如图,在△OAB中,点P是线段OB及线段AB延长线所围成的阴影区域(含边界)的任意一点,且 1、如图,在直角坐标平面内有一个边长为a,中心在原点O的正六边形ABCDEF,AB∥Ox.直线L:y=kx+t(k为常数)与正六边形交于M、N两点,记△OMN的面积为S,则函数S=f(t)的奇偶性为
1、如图,在直角坐标平面内有一个边长为a,中心在原点O的正六边形ABCDEF,AB∥Ox.直线L:y=kx+t(k为常数)与正六边形交于M、N两点,记△OMN的面积为S,则函数S=f(t)的奇偶性为
 (2008•海珠区一模)如图,在直角坐标平面内,射线OT落在60°的终边上,任作一条射线OA,OA落在∠xOT内的概率是
(2008•海珠区一模)如图,在直角坐标平面内,射线OT落在60°的终边上,任作一条射线OA,OA落在∠xOT内的概率是