题目内容
已知动点P(x，y)在椭圆
+
=1上，若A点坐标为(1，0)，|
|=1且
•
=0，则|
|的最小值是
．
| x2 |
| 25 |
| y2 |
| 16 |
| AM |
| PM |
| AM |
| PM |
| ||
| 3 |
| ||
| 3 |
分析：由题意可知点M的轨迹为以点A为圆心，1为半径的圆，PM为圆的切线，则|PM|2=|PA|2-1，要使得|
|的值最小，则要
的值最小，而
的最小值，根据椭圆的性质可求．
| PM |
| PA |
| PA |
解答：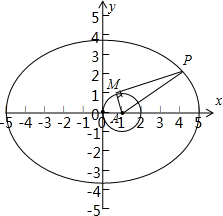
解：由||
||=1可知点M的轨迹为以点A为圆心，1为半径的圆，
∵
•
=0
∴过点P作该圆的切线PM，则|PA|2=|PM|2+|AM|2，得|PM|2=|PA|2-1，
∴要使得|
|的值最小，则要|
|的值最小，
因为P(x，y)在
+
=1上，
而|
|=
=
，当x=
时|
|取得最小值为：
，
此时|
|=
=
=
，
故答案为：
．
解：由||| PM |
∵
| PM |
| AM |
∴过点P作该圆的切线PM，则|PA|2=|PM|2+|AM|2，得|PM|2=|PA|2-1，
∴要使得|
| PM |
| PA |
因为P(x，y)在
| x2 |
| 25 |
| y2 |
| 16 |
而|
| PA |
| (x-1)2+y2 |
|
| 25 |
| 9 |
| PA |
|
此时|
| PM |
| |PA|2-|AM|2 |
|
| ||
| 3 |
故答案为：
| ||
| 3 |
点评：本题考查求最值过程中利用三角形两边之差小于等于第三边来取得最值，又要结合椭圆的定义，很关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
上，若A点坐标为(3，0)，
且
，则
的最小值是________．
，O为坐标原点，定点A(6，8)，则
在
上的投影的范围
]
]
]
．