题目内容
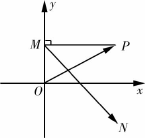
已知动点P(x,y)到原点的距离的平方与它到直线l:x=m (m是常数)的距离相等.
(1)求动点P的轨迹方程C;
(2)就m的不同取值讨论轨迹方程C的图形.
(2)就m的不同取值讨论轨迹方程C的图形.
解:(1)因为原点O(0,0),
所以动点P(x,y)到原点的距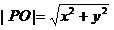 ,
,
于是动点P的坐标满足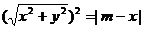
∴x2+y2=|m-x|,此即为动点P的轨迹方程C.
(2)由x2+y2=|m-x|,两边平方,移项因式分解,得(x2+y-m+x)(x2+y2+m-x)=0,
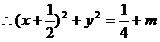 或
或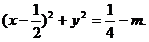
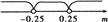
①当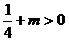 .且
.且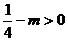 .
.
即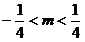 时,
时,
点P的轨迹是两个圆,一个圆的圆心是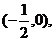 半径为
半径为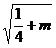 ;
;
一个圆的圆心是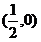 ,半径为
,半径为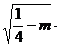
②当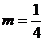 或
或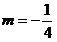 时,点P的轨迹是一个圆和一个点,
时,点P的轨迹是一个圆和一个点,
③当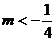 或
或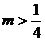 时,点P的轨迹是一个圆.
时,点P的轨迹是一个圆.
所以动点P(x,y)到原点的距
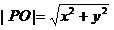 ,
,于是动点P的坐标满足
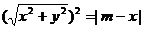
∴x2+y2=|m-x|,此即为动点P的轨迹方程C.
(2)由x2+y2=|m-x|,两边平方,移项因式分解,得(x2+y-m+x)(x2+y2+m-x)=0,
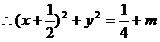 或
或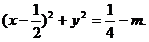

①当
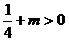 .且
.且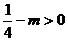 .
.即
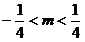 时,
时,点P的轨迹是两个圆,一个圆的圆心是
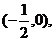 半径为
半径为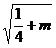 ;
;一个圆的圆心是
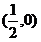 ,半径为
,半径为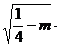
②当
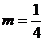 或
或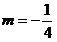 时,点P的轨迹是一个圆和一个点,
时,点P的轨迹是一个圆和一个点,③当
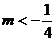 或
或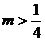 时,点P的轨迹是一个圆.
时,点P的轨迹是一个圆.
练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
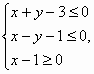 ,O为坐标原点,定点A(6,8),则
,O为坐标原点,定点A(6,8),则