题目内容
设P=1+5（x+1）+10（x+1）2+10（x+1）3+5（x+1）4+（x+1）5，化简后P=
- A.x5
- B.（x+2）5
- C.（x-1）5
- D.（x+1）5
B
分析：分析所给代数式的特点，可得所求的式子恰好是[1+（x+1）]5的展开式，从而得出结论．
解答：由于 P=1+5（x+1）+10（x+1）2+10（x+1）3+5（x+1）4+（x+1）5 =[1+（x+1）]5=（x+2）5，
故选B．
点评：本题主要考查二项式定理的应用，判断要求的式子恰好是[1+（x+1）]5的展开式，是解题的关键，属于基础题．
分析：分析所给代数式的特点，可得所求的式子恰好是[1+（x+1）]5的展开式，从而得出结论．
解答：由于 P=1+5（x+1）+10（x+1）2+10（x+1）3+5（x+1）4+（x+1）5 =[1+（x+1）]5=（x+2）5，
故选B．
点评：本题主要考查二项式定理的应用，判断要求的式子恰好是[1+（x+1）]5的展开式，是解题的关键，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
x∈R，使得x2+1＞3x”的否定是“ 
x∈R，都有x2+1＜3x”；
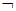p∧