题目内容
设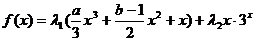
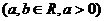 .
.
(1)当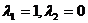 ,设x1,x2是f(x)的两个极值点,且满足x1<1<x2<2,求证:
,设x1,x2是f(x)的两个极值点,且满足x1<1<x2<2,求证: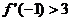 ;
;
(2)当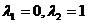 时,
时,
①求函数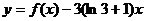 (x>0)的最小值;
(x>0)的最小值;
②对于任意正实数a,b,c,当a+b+c=3时,求证:3aa+3bb+3cc≥9.
【答案】
(1)当λ1=1,λ2=0,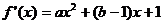
x1,x2是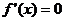 两根,由x1<1<x2<2,a>0
两根,由x1<1<x2<2,a>0
∴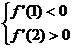 即
即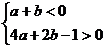
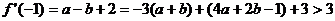 …4分
…4分
(2)①当λ1=0,λ2=1时,f(x)=3x·x y=3x·x-3(ln3+1)x
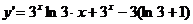
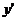 是增函数,且x=1是它的一个零点,即也是唯一的一个零点
是增函数,且x=1是它的一个零点,即也是唯一的一个零点
当x>1时,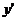 >0,当0<x<1时,
>0,当0<x<1时,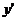 <0
<0
∴ 当x=1时,y=f(x)-3(ln3+1)x有最小值为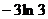 ……8分
……8分
②由①知:3xx≥3(ln3+1)x-3ln3,当x分别取a,b,c时有
3aa≥3(ln3+1)a-3ln3
3bb≥3(ln3+1)b-3ln3
3Cc≥3(ln3+1)c-3ln3 三式相加即得 …………14分

练习册系列答案
相关题目
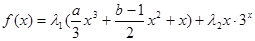
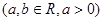 .
.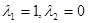 ,设x1,x2是f(x)的两个极值点,且满足x1<1<x2<2,求证:
,设x1,x2是f(x)的两个极值点,且满足x1<1<x2<2,求证: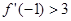 ;
;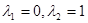 时,
时,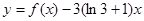 (x>0)的最小值;
(x>0)的最小值;