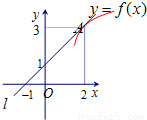题目内容
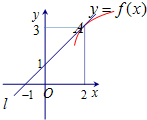已知直线l经过（-1，0），（0，1）两点，且与曲线y=f（x）切于点A（2，3），则| lim |
| △x→0 |
| f(2+△x)-f(2) |
| △x |
分析：直线l经过（-1，0），（0，1）两点，可以写出直线l的方程，根据导数的几何意义进行求解；
解答：解：∵直线l经过（-1，0），（0，1）两点，
可得l：y=x+1，
直线与曲线y=f（x）切于点A（2，3），可得曲线在x=2处的导数为：f′（2）=1，
又根据导数的定义：f′（2）=
=1，
故选C；
可得l：y=x+1，
直线与曲线y=f（x）切于点A（2，3），可得曲线在x=2处的导数为：f′（2）=1，
又根据导数的定义：f′（2）=
| lim |
| △x→0 |
| f(2+△x)-f(2) |
| △x |
故选C；
点评：本题以函数为载体，考查导数的几何意义，关键是理解导数的定义，从而得解，是一道基础题；
练习册系列答案
名师伴你成长课时同步学练测系列答案
相关题目
,5) B.(15,40) C.(t,3t-5) D.(3t-5,t)
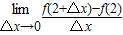的值为（ ）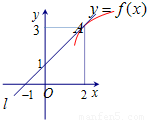
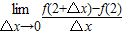的值为（ ）