题目内容
已知△ABC中，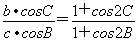
，试判断△ABC的形状．
三角形为等腰或直角三角形
【解析】由已知，得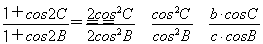
，∴
.
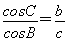由正弦定理知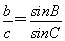
，∴
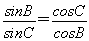.∴sinCcosC＝sinBcosB，即sin2C＝sin2B，因为∠B、∠C均为△ABC的内角．所以2∠C＝2∠B或2∠C＋2∠B＝180°，所以∠B＝∠C或∠B＋∠C＝90°，故三角形为等腰或直角三角形．
练习册系列答案
名校课堂系列答案
相关题目
名校课堂系列答案题目内容
已知△ABC中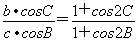，，试判断△ABC的形状．
三角形为等腰或直角三角形
【解析】由已知，得，∴.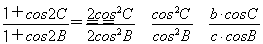
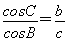由正弦定理知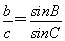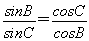，∴.∴sinCcosC＝sinBcosB，即sin2C＝sin2B，因为∠B、∠C均为△ABC的内角．所以2∠C＝2∠B或2∠C＋2∠B＝180°，所以∠B＝∠C或∠B＋∠C＝90°，故三角形为等腰或直角三角形．
名校课堂系列答案
