题目内容
若函数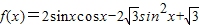
(Ⅰ)求f(x)的最小正周期;
(Ⅱ)当x
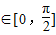 时,求函数f(x)的最大值与最小值.
时,求函数f(x)的最大值与最小值.
【答案】分析:(Ⅰ)由倍角公式和两角和的正弦公式化简解析式,再由周期公式求出函数的周期;
(Ⅱ)求x的范围求出 的范围,由正弦函数的性质求出
的范围,由正弦函数的性质求出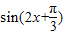 的范围,再求函数的最大值和最小值.
的范围,再求函数的最大值和最小值.
解答:解:(Ⅰ)由题意得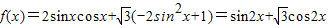
=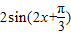 ,
,
∴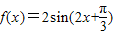 ,∴函数的周期是
,∴函数的周期是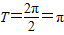 ,
,
(Ⅱ)∵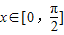 ,∴
,∴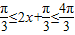
则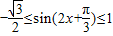 ,
,
∴ .
.
点评:本题考查了倍角公式、两角和的正弦公式,正弦函数的性质的应用,考查了整体思想.
(Ⅱ)求x的范围求出
 的范围,由正弦函数的性质求出
的范围,由正弦函数的性质求出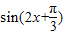 的范围,再求函数的最大值和最小值.
的范围,再求函数的最大值和最小值.解答:解:(Ⅰ)由题意得
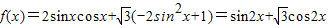
=
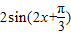 ,
,∴
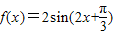 ,∴函数的周期是
,∴函数的周期是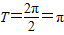 ,
,(Ⅱ)∵
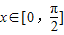 ,∴
,∴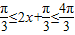
则
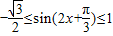 ,
,∴
 .
.点评:本题考查了倍角公式、两角和的正弦公式,正弦函数的性质的应用,考查了整体思想.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
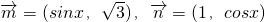 ,若函数
,若函数
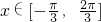 时,求f(x)的减区间.
时,求f(x)的减区间.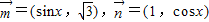 ,若函数
,若函数
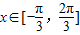 时,求f(x)的减区间.
时,求f(x)的减区间.