题目内容
已知函数f(x)在定义域内是递减函数,且f(x)<0恒成立,给出下列函数:①y=-5+f(x);②y=
;③y=5-
;④y=[f(x)]2;其中在其定义域内单调递增的函数的序号是
| -f(x) |
| 1 |
| f(x) |
②④
②④
.分析:先判断函数的定义域,再确定其单调性.①中,y=-5+f(x)与f(x)的单调性相同;
②f(x)<0,-f(x)>0,且在其定义域内单调递增;
③中函数的导数
在其定义域内单调递增,故y=5-
在定义域内是递减函数;
④中y=[f(x)]2,两个减函数的积,在其公共定义域内为增函数,从而可得答案.
②f(x)<0,-f(x)>0,且在其定义域内单调递增;
③中函数的导数
| 1 |
| f(x) |
| 1 |
| f(x) |
④中y=[f(x)]2,两个减函数的积,在其公共定义域内为增函数,从而可得答案.
解答:解:由题意,函数f(x)在定义域内是递减函数,且f(x)<0恒成立
对于①:y=-5+f(x)在定义域内是递减函数,故不符合;
对于②f(x)<0,-f(x)>0,且在其定义域内单调递增,故符合;
对于③
在其定义域内单调递增,故y=5-
在定义域内是递减函数,故不符合;
对于④y=[f(x)]2,两个减函数的积,在其公共定义域内为增函数,故符合
故答案为:②④
对于①:y=-5+f(x)在定义域内是递减函数,故不符合;
对于②f(x)<0,-f(x)>0,且在其定义域内单调递增,故符合;
对于③
| 1 |
| f(x) |
| 1 |
| f(x) |
对于④y=[f(x)]2,两个减函数的积,在其公共定义域内为增函数,故符合
故答案为:②④
点评:本题以函数为载体,考查函数的单调性,注意正确判别函数之间的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
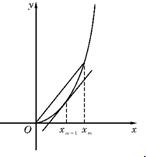 已知函数f(x)=x3+x2,数列|xn|(xn>0)的第一项xn=1,以后各项按如下方式取定:曲线x=f(x)在(xn+1,f(xn+1))处的切线与经过(0,0)和(xn,f (xn))两点的直线平行(如图).
已知函数f(x)=x3+x2,数列|xn|(xn>0)的第一项xn=1,以后各项按如下方式取定:曲线x=f(x)在(xn+1,f(xn+1))处的切线与经过(0,0)和(xn,f (xn))两点的直线平行(如图).
 中ξi的选取是任意的,且In仅于n有关.
中ξi的选取是任意的,且In仅于n有关.