题目内容
因金融危机,某公司的出口额下降,为此有关专家提出两种促进出口的方案,每种方案都需要分两年实施.若实施方案一,预计第一年可以使出口额恢复到危机前的1.0倍、0.9倍、0.8倍的概率分别为0.3、0.3、0.4;第二年可以使出口额为第一年的1.25倍、1.0倍的概率分别是0.5、0.5.若实施方案二,预计第一年可以使出口额恢复到危机前的1.2倍、l.0倍、0.8倍的概率分别为0.2、0.3、0.5;第二年可以使出口额为第一年的1.2倍、1.0倍的概率分别是0.4、0.6.实施每种方案第一年与第二年相互独立.令ξ1(=1,2)表示方案实施两年后出口额达到危机前的倍数.
(Ⅰ)写出ξ1、ξ2的分布列;
(Ⅱ)实施哪种方案,两年后出口额超过危机前出口额的概率更大?
(Ⅲ)不管哪种方案,如果实施两年后出口额达不到、恰好达到、超过危机前出口额,预计利润分别为10万元、15万元、20万元,问实施哪种方案的平均利润更大.
解:(Ⅰ)ξ1的所有取值为0.8,0.9,1.0,1.125,1.25,
其分布列为:
…(2分)
ξ2的所有取值为0.8,0.96,1.0,1,2,1.44,其分布列为
…(4分)
(Ⅱ)设实施方案一、方案二两年后超过危机前出口额的概率为P1,P2,则P1=0.15+0.15=0.3,P2=0.24+0.08=0.32
∴实施方案二两年后超过危机前出口额的概率更大.…(6分)
(Ⅲ)方案一、方案二的预计利润为η1、η2,则
…(8分)
…(10分)
∴Eη1=14.75Eη2=14.1
∴实施方案一的平均利润更大.…(12分)
分析:(Ⅰ)确定ξ1、ξ2的所有可能取值,求出概率,即可得到分布列;
(Ⅱ)求出倍数大于1的概率,利用互斥事件的概率公式,即可得到结论;
(Ⅲ)分别求出利润分别为10万元、15万元、20万元时的概率,再计算期望,即可求得结论.
点评:本题考查概率的计算,考查离散型随机变量的分布列与期望,确定变量的取值,求出概率是关键.
其分布列为:
| ξ1 | 0.8 | 0.9 | 1.0 | 1.125 | 1.25 |
| P | 0.2 | 0.15 | 0.35 | 0.15 | 0.15 |
ξ2的所有取值为0.8,0.96,1.0,1,2,1.44,其分布列为
| ξ2 | 0.8 | 0.96 | 1.0 | 1.2 | 1.44 |
| P | 0.3 | 0.2 | 0.18 | 0.24 | 0.08 |
(Ⅱ)设实施方案一、方案二两年后超过危机前出口额的概率为P1,P2,则P1=0.15+0.15=0.3,P2=0.24+0.08=0.32
∴实施方案二两年后超过危机前出口额的概率更大.…(6分)
(Ⅲ)方案一、方案二的预计利润为η1、η2,则
| η1 | 10 | 15 | 20 |
| P | 0.35 | 0.35 | 0.3 |
| η2 | 10 | 15 | 20 |
| P | 0. 5 | 0.18 | 0.32 |
∴Eη1=14.75Eη2=14.1
∴实施方案一的平均利润更大.…(12分)
分析:(Ⅰ)确定ξ1、ξ2的所有可能取值,求出概率,即可得到分布列;
(Ⅱ)求出倍数大于1的概率,利用互斥事件的概率公式,即可得到结论;
(Ⅲ)分别求出利润分别为10万元、15万元、20万元时的概率,再计算期望,即可求得结论.
点评:本题考查概率的计算,考查离散型随机变量的分布列与期望,确定变量的取值,求出概率是关键.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
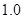 倍、
倍、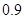 倍、
倍、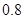 倍的概率分别为
倍的概率分别为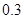 、
、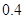 ;第二年可以使出口额为第一年的
;第二年可以使出口额为第一年的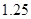 倍、
倍、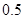 、
、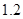 倍、
倍、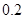 、
、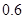 。实施每种方案第一年与第二年相互独立。令
。实施每种方案第一年与第二年相互独立。令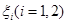 表示方案
表示方案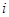 实施两年后出口额达到危机前的倍数。
实施两年后出口额达到危机前的倍数。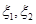 的分布列;
的分布列;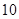 万元、
万元、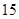 万元、
万元、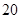 万元,问实施哪种方案的平均利润更大?
万元,问实施哪种方案的平均利润更大?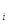 (
(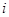 =1,2)表示方案
=1,2)表示方案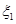 、
、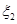 的分布列;
的分布列;