题目内容
设集合A为函数y=ln(-x2-2x+8)的定义域,集合B为函数的值域,集合C为不等式(ax-
![]() )(x+4)≤0的解集. (1)求A∩B; (2)若C⊆∁RA,求a的取值范围.
)(x+4)≤0的解集. (1)求A∩B; (2)若C⊆∁RA,求a的取值范围.
解:(1)由-x2-2x+8>0,解得A=(-4,2),又y=x+![]() =(x+1)+
=(x+1)+![]() -1,
-1,
所以B=(-∞,-3]∪ [1,+∞).所以A∩B=(-4,-3]∪[1,2).
(2)因为∁RA=(-∞,-4]∪[2,+∞).
由![]() (x+4)≤0,知a≠0.
(x+4)≤0,知a≠0.
①当a>0时,由![]() (x+4)≤0,得C=
(x+4)≤0,得C=![]() ,不满足C⊆∁RA;
,不满足C⊆∁RA;
②当a<0时,由![]() (x+4)≥0,得C=(-∞,-4)∪
(x+4)≥0,得C=(-∞,-4)∪![]() ,
,
欲使C⊆∁RA,则![]() ≥2,
≥2,
解得-![]() ≤a<0或0<a≤
≤a<0或0<a≤![]() .又a<0,所以-
.又a<0,所以-![]() ≤a<0.
≤a<0.
综上所述,所求a的取值范围是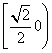 .
.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
 的值域,集合C为不等式(ax-
的值域,集合C为不等式(ax-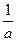 )(x+4)≤0的解集. (1)求A∩B; (2)若C⊆∁RA,求a的取值范围.
)(x+4)≤0的解集. (1)求A∩B; (2)若C⊆∁RA,求a的取值范围. 的值域,集合C为不等式(ax-
的值域,集合C为不等式(ax- )(x+4)≤0的解集.
)(x+4)≤0的解集. 的值域,集合C为不等式(ax-
的值域,集合C为不等式(ax- )(x+4)≤0的解集. (1)求A∩B; (2)若C⊆∁RA,求a的取值范围.
)(x+4)≤0的解集. (1)求A∩B; (2)若C⊆∁RA,求a的取值范围.