题目内容
三棱锥P-ABC的两侧面PAB,PBC都是边长为2的正三角形,AC=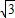 ,则二面角A-PB-C的大小为 .
,则二面角A-PB-C的大小为 .
【答案】分析:取PB的中点M,连接AM,CM,可得∠AMC为二面角A-PB-C的平面角,在△AMC中可得△AMC为正三角形,从而求出∠AMC即可得到二面角A-PB-C的大小.
解答: 解:取PB的中点M,连接AM,CM.
解:取PB的中点M,连接AM,CM.
则AM⊥PB,CM⊥PB.
故∠AMC为二面角A-PB-C的平面角.
在△AMC中可得AM=CM= ,而AC=
,而AC=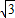 ,则△AMC为正三角形,
,则△AMC为正三角形,
∴∠AMC=60°,
∴二面角A-PB-C的大小为60°,
故答案为60°.
点评:本小题主要考查棱锥的结构特征、二面角解法等基础知识,考查运算求解能力,属于中档题.
解答:
 解:取PB的中点M,连接AM,CM.
解:取PB的中点M,连接AM,CM.则AM⊥PB,CM⊥PB.
故∠AMC为二面角A-PB-C的平面角.
在△AMC中可得AM=CM=
 ,而AC=
,而AC=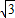 ,则△AMC为正三角形,
,则△AMC为正三角形,∴∠AMC=60°,
∴二面角A-PB-C的大小为60°,
故答案为60°.
点评:本小题主要考查棱锥的结构特征、二面角解法等基础知识,考查运算求解能力,属于中档题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
 a,则二面角A-PB-C的大小为
a,则二面角A-PB-C的大小为 a,则二面角A-PB-C的大小为( )
a,则二面角A-PB-C的大小为( )