题目内容
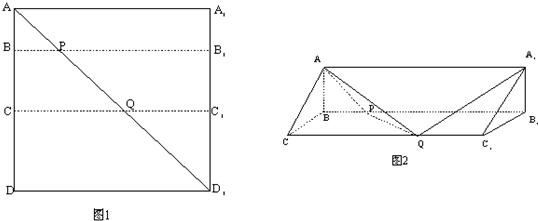
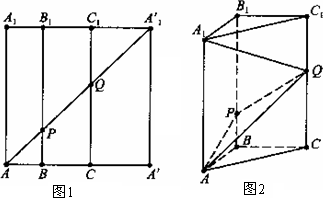
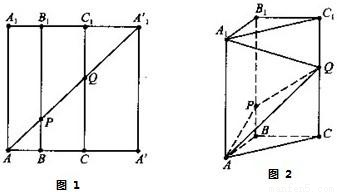
如图1，在边长为12的正方形AA′A′1A1中，BB1∥CC1∥AA1，且AB=3，BC=4，AA′1分别交BB1，CC1于点P、Q，将该正方形沿BB1、CC1折叠，使得A′A′1与AA1重合，构成如图2所示的三棱柱ABC-A1B1C1，请在图2中解决下列问题：
（1）求证：AB⊥PQ；
（2）在底边AC上有一点M，满足AM；MC=3：4，求证：BM∥平面APQ．
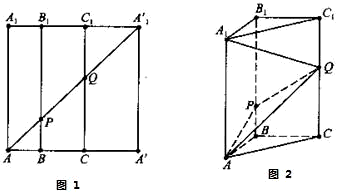
（1）证明：因为AB=3，BC=4，
所以AC=5，从而AC2=AB2+BC2，
即AB⊥BC．（3分）
又因为AB⊥BB1，而BC∩BB1=B，
所以AB⊥平面BC1，又PQ?平面BC1
所以AB⊥PQ （6分）
（2）证明：过M作MN∥CQ交AQ于N，连接PN，
因为AM：MC=3：4∴AM：AC=MN：CQ=3：7 （9分）
∴MN=PB=3∵PB∥CQ∴MN∥PB∴四边形PBMN为平行四边形
∴BM∥PN，所以BM∥平面APQ．（12分）
分析：（1）根据AB，BC，AC三边满足AC2=AB2+BC2，可知AB⊥BC，而AB⊥BB1，BC∩BB1=B，根据线面垂直的判定定理可知AB⊥平面BC1，又PQ?平面BC1，根据线面垂直的性质可知AB⊥PQ；
（2）欲证BM∥平面APQ，根据直线与平面平行的判定定理可知只需证BM与平面APQ内一直线平行即可，过M作MN∥CQ交AQ于N，连接PN，
根据边的比例关系可证得四边形PBMN为平行四边形，从而BM∥PN，满足定理所需条件．
点评：本题主要考查了空间两直线的位置关系的判定，以及直线与平面平行的判定，同时考查了空间想象能力和推理能力，属于中档题．
所以AC=5，从而AC2=AB2+BC2，
即AB⊥BC．（3分）
又因为AB⊥BB1，而BC∩BB1=B，
所以AB⊥平面BC1，又PQ?平面BC1
所以AB⊥PQ （6分）
（2）证明：过M作MN∥CQ交AQ于N，连接PN，
因为AM：MC=3：4∴AM：AC=MN：CQ=3：7 （9分）
∴MN=PB=3∵PB∥CQ∴MN∥PB∴四边形PBMN为平行四边形
∴BM∥PN，所以BM∥平面APQ．（12分）
分析：（1）根据AB，BC，AC三边满足AC2=AB2+BC2，可知AB⊥BC，而AB⊥BB1，BC∩BB1=B，根据线面垂直的判定定理可知AB⊥平面BC1，又PQ?平面BC1，根据线面垂直的性质可知AB⊥PQ；
（2）欲证BM∥平面APQ，根据直线与平面平行的判定定理可知只需证BM与平面APQ内一直线平行即可，过M作MN∥CQ交AQ于N，连接PN，
根据边的比例关系可证得四边形PBMN为平行四边形，从而BM∥PN，满足定理所需条件．
点评：本题主要考查了空间两直线的位置关系的判定，以及直线与平面平行的判定，同时考查了空间想象能力和推理能力，属于中档题．
练习册系列答案
相关题目
中，BB1∥CC1∥AA1，且AB＝3，BC＝4，
分别交BB1，CC1于点P、Q，将该正方形沿BB1、CC1折叠，使得
与AA1重合，构成如图2所示的三棱柱ABC－A1B1C1，请在图2中解决下列问题：
