题目内容
若不等式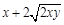
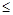 a(x+y) 对一切正数x、y恒成立,则正数a的最小值为( )
a(x+y) 对一切正数x、y恒成立,则正数a的最小值为( )
| A. 1; | B.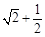 ; ; | C. 2; | D.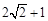 ; ; |
C
解析试题分析:∵不等式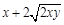
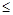 a(x+y) 对一切正数x、y恒成立,∴a≥
a(x+y) 对一切正数x、y恒成立,∴a≥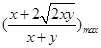 .
.
令f(x,y)=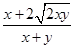 =
=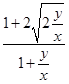 ,x>0,y>0.
,x>0,y>0.
令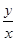 =t>0,则g(t)=
=t>0,则g(t)=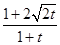 ,g′(t)=
,g′(t)=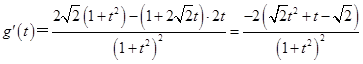
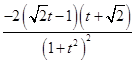 ,令g′(t)=0,解得t=
,令g′(t)=0,解得t=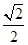 ,可知当t=
,可知当t=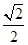 时,g(t)取得极大值即最大值,
时,g(t)取得极大值即最大值,
g(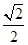 )=
)=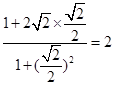 ,∴a≥2.故a的最小值为2.故选C.
,∴a≥2.故a的最小值为2.故选C.
考点:恒成立问题的等价转化、利用导数研究函数的单调性极值与最值等基础知识与基本技能方法

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设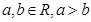 ,则下列不等式一定成立的是( )
,则下列不等式一定成立的是( )
A.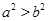 | B.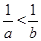 | C.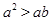 | D. |
下列推理正确的是( )
| A.如果不买彩票,那么就不能中奖.因为你买了彩票,所以你一定中奖 |
| B.因为a>b,a>c,所以a-b>a-c |
C.若a>0,b>0,则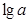 + +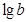 ≥ ≥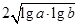 |
D.若a>0,b<0,则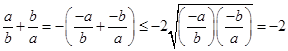 |
已知 且
且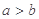 ,则下列不等式中成立的是( )
,则下列不等式中成立的是( )
A. | B.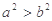 | C.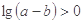 | D.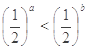 |
方程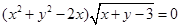 表示的曲线是( )
表示的曲线是( )
| A.一个圆和一条直线 | B.一个圆和一条射线 | C.一个圆 | D.一条直线 |
[2014·银川质检]当x∈(0,+∞)时可得到不等式x+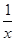 ≥2,x+
≥2,x+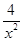 =
=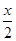 +
+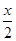 +(
+(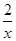 )2≥3,由此可以推广为x+
)2≥3,由此可以推广为x+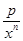 ≥n+1,取值p等于 ( )
≥n+1,取值p等于 ( )
| A.nn | B.n2 | C.n | D.n+1 |
“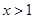 ”是“
”是“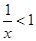 ”的( )
”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
若a,b是任意实数,且a>b,则 ( )
| A.a2>b2 | B. <1 <1 |
| C.lg(a-b)>0 | D.( )a<( )a<( )b )b |
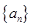 是公差为2的等差数列,
是公差为2的等差数列,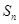 是
是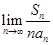 = .
= .