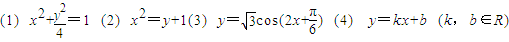题目内容
若一条曲线既是轴对称图形又是中心对称图形,则称此曲线为双重对称曲线,下列四条曲线①
+
=1,②x2-y2=1,③y=x2④y=sinx中,双重对称曲线的序号是 .
| x2 |
| 25 |
| y2 |
| 16 |
分析:通过将方程中的x换为-x,y换为y方程不变,判断出①②中的曲线为双重对称曲线,根据抛物线只有对称轴无对称中心,判断出③不是双重对称曲线,通过正弦函数的性质判断出④中的曲线为双重对称曲线.
解答:解:对于①,将x换为-x,y换为y方程不变,所以①
+
=1关于x,y轴对称且关于原点对称,所以①对;
对于②,将x换为-x,y换为y方程不变,所以x2-y2=1关于x,y轴对称且关于原点对称,所以②对;
对于③,y=x2表示的是顶点在原点,关于y轴对称的抛物线,无对称中心,所以③不对;
对于④,正弦函数y=sinx的对称中心为(kπ,0);对称轴为x=kπ+
,所以④对.
故答案为①②④
| x2 |
| 25 |
| y2 |
| 16 |
对于②,将x换为-x,y换为y方程不变,所以x2-y2=1关于x,y轴对称且关于原点对称,所以②对;
对于③,y=x2表示的是顶点在原点,关于y轴对称的抛物线,无对称中心,所以③不对;
对于④,正弦函数y=sinx的对称中心为(kπ,0);对称轴为x=kπ+
| π |
| 2 |
故答案为①②④
点评:本题考查判断一条曲线是否关于x,y轴对称及是否关于原点对称的判断方法,是一道基础题.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目