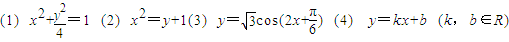题目内容
若一条曲线既是轴对称图形，又是中心对称图形，则称这条曲线为“二重对称曲线”，给出下列四条曲线：(1) x2+
=1 (2) x2=y+1(3) y=
cos(2x+
) (4) y=kx+b (k，b∈R)
其中是“二重对称曲线”的有______．
| y2 |
| 4 |
| 3 |
| π |
| 6 |
其中是“二重对称曲线”的有______．
（1）由题意可得方程x2+
=1表示椭圆，由椭圆的性质可得椭圆即关于x轴，y轴对称也关于原点对称，所以曲线x2+
=1是二重对称曲线，所以选（1）．
（2）由x2=y+1可得y=x2-1，所以函数y=x2-1是二次函数，由二次函数的性质可得其只有对称轴，所以曲线x2=y+1不是二重对称曲线，所以不选（2）．
（3）函数y=
cos(2x+
)的图象由余弦函数的图象平移变换而来，因为余弦函数的图象有对称轴与对称中心．所以可得曲线y=
cos(2x+
)是二重对称曲线，所以选（3）．
（4）由一次函数的性质可得：只有当k=0时，曲线y=kx+b（k，b∈R）才有对称轴与对称中心，所以曲线y=kx+b（k，b∈R）不是二重对称曲线，所以不选（4）．
故答案为：（1）（3）．
| y2 |
| 4 |
| y2 |
| 4 |
（2）由x2=y+1可得y=x2-1，所以函数y=x2-1是二次函数，由二次函数的性质可得其只有对称轴，所以曲线x2=y+1不是二重对称曲线，所以不选（2）．
（3）函数y=
| 3 |
| π |
| 6 |
| 3 |
| π |
| 6 |
（4）由一次函数的性质可得：只有当k=0时，曲线y=kx+b（k，b∈R）才有对称轴与对称中心，所以曲线y=kx+b（k，b∈R）不是二重对称曲线，所以不选（4）．
故答案为：（1）（3）．
练习册系列答案
阅读快车系列答案
相关题目
B．
D．