题目内容
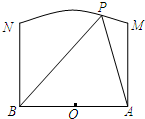 如图,两个工厂A,B相距2km,点O为AB的中点,现要在以O为圆心,2km为半径的圆弧MN上的某一点P处建一幢办公楼,其中MA⊥AB,NB⊥AB.据测算此办公楼受工厂A的“噪音影响度”与距离AP的平方成反比,比例系数是1,办公楼受工厂B的“噪音影响度”与距离BP的平方也成反比,比例系数是4,办公楼受A,B两厂的“总噪音影响度”y是受A,B两厂“噪音影响度”的和,设AP为xkm.
如图,两个工厂A,B相距2km,点O为AB的中点,现要在以O为圆心,2km为半径的圆弧MN上的某一点P处建一幢办公楼,其中MA⊥AB,NB⊥AB.据测算此办公楼受工厂A的“噪音影响度”与距离AP的平方成反比,比例系数是1,办公楼受工厂B的“噪音影响度”与距离BP的平方也成反比,比例系数是4,办公楼受A,B两厂的“总噪音影响度”y是受A,B两厂“噪音影响度”的和,设AP为xkm.
(Ⅰ)求“总噪音影响度”y关于x的函数关系,并求出该函数的定义域;
(Ⅱ)当AP为多少时,“总噪音影响度”最小?
解:(Ⅰ)连接OP,设∠AOP=α,则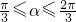 ;
;
在△AOP中,由余弦定理得x2=12+22-2×1×2cosα=5-4cosα,
在△BOP中,由余弦定理得BP2=12+22-2×1×2cos(π-α)=5+4cosα,
∴BP2=10-x2.则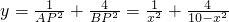 ;
;
∵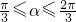 ,则
,则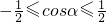 ,∴3≤5-4cosα≤7,
,∴3≤5-4cosα≤7,
∴ ;
;
所以,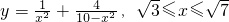 .
.
(Ⅱ)令t=x2,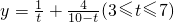 ;
;
∴ ;
;
由y'=0,得 ,或t=-10(舍去),
,或t=-10(舍去),
当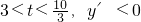 ,函数在
,函数在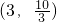 上单调递减;
上单调递减;
当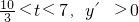 ,函数在
,函数在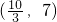 上单调递增;
上单调递增;
∴当 时,即
时,即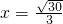 时,函数有最小值,
时,函数有最小值,
也即当AP为 km时,“总噪音影响度”最小.
km时,“总噪音影响度”最小.
分析:(Ⅰ)连接OP,设∠AOP=α,在△AOP中,由余弦定理得x2,在△BOP中,由余弦定理得BP2,从而得BP与x的关系,所以,“总噪音影响度”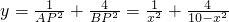 ;定义域由∠α的取值得出x的取值范围即可.
;定义域由∠α的取值得出x的取值范围即可.
(Ⅱ)用换元法,令t=x2,则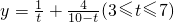 ;对y求导,令y'=0,得
;对y求导,令y'=0,得 时,函数有最小值,
时,函数有最小值,
即AP= (km)时,“总噪音影响度”最小即可.
(km)时,“总噪音影响度”最小即可.
点评:本题考查了余弦定理的应用和导数在求函数最值问题中的应用;用求导法求函数最值时,要先求导,再令导数等于0,并判断导数等于0的点是否为最值点.
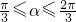 ;
;在△AOP中,由余弦定理得x2=12+22-2×1×2cosα=5-4cosα,
在△BOP中,由余弦定理得BP2=12+22-2×1×2cos(π-α)=5+4cosα,
∴BP2=10-x2.则
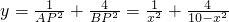 ;
;∵
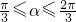 ,则
,则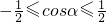 ,∴3≤5-4cosα≤7,
,∴3≤5-4cosα≤7,∴
 ;
;所以,
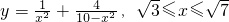 .
.(Ⅱ)令t=x2,
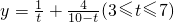 ;
;∴
 ;
;由y'=0,得
 ,或t=-10(舍去),
,或t=-10(舍去),当
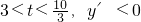 ,函数在
,函数在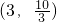 上单调递减;
上单调递减;当
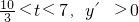 ,函数在
,函数在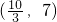 上单调递增;
上单调递增;∴当
 时,即
时,即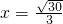 时,函数有最小值,
时,函数有最小值,也即当AP为
 km时,“总噪音影响度”最小.
km时,“总噪音影响度”最小.分析:(Ⅰ)连接OP,设∠AOP=α,在△AOP中,由余弦定理得x2,在△BOP中,由余弦定理得BP2,从而得BP与x的关系,所以,“总噪音影响度”
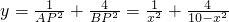 ;定义域由∠α的取值得出x的取值范围即可.
;定义域由∠α的取值得出x的取值范围即可.(Ⅱ)用换元法,令t=x2,则
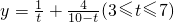 ;对y求导,令y'=0,得
;对y求导,令y'=0,得 时,函数有最小值,
时,函数有最小值,即AP=
 (km)时,“总噪音影响度”最小即可.
(km)时,“总噪音影响度”最小即可.点评:本题考查了余弦定理的应用和导数在求函数最值问题中的应用;用求导法求函数最值时,要先求导,再令导数等于0,并判断导数等于0的点是否为最值点.

练习册系列答案
相关题目
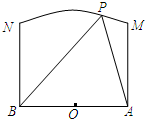 如图,两个工厂A,B相距2km,点O为AB的中点,现要在以O为圆心,2km为半径的圆弧MN上的某一点P处建一幢办公楼,其中MA⊥AB,NB⊥AB.据测算此办公楼受工厂A的“噪音影响度”与距离AP的平方成反比,比例系数是1,办公楼受工厂B的“噪音影响度”与距离BP的平方也成反比,比例系数是4,办公楼受A,B两厂的“总噪音影响度”y是受A,B两厂“噪音影响度”的和,设AP为xkm.
如图,两个工厂A,B相距2km,点O为AB的中点,现要在以O为圆心,2km为半径的圆弧MN上的某一点P处建一幢办公楼,其中MA⊥AB,NB⊥AB.据测算此办公楼受工厂A的“噪音影响度”与距离AP的平方成反比,比例系数是1,办公楼受工厂B的“噪音影响度”与距离BP的平方也成反比,比例系数是4,办公楼受A,B两厂的“总噪音影响度”y是受A,B两厂“噪音影响度”的和,设AP为xkm.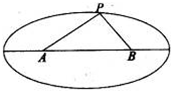 如图,两个工厂A,B(视为两个点)相距2km,现要在以A,B为焦点,长轴长为4km的椭圆上某一点P处建一幢办公楼.据测算此办公楼受工厂A的“噪音影响度”与距离AP成反比,比例系数是1;办公楼受工厂B的“噪音影响度”与距离BP也成反比,比例系数是4.办公楼受A,B两厂的“总噪音影响度”y是受A,B两厂“噪音影响度”的和,设AP=xkm.
如图,两个工厂A,B(视为两个点)相距2km,现要在以A,B为焦点,长轴长为4km的椭圆上某一点P处建一幢办公楼.据测算此办公楼受工厂A的“噪音影响度”与距离AP成反比,比例系数是1;办公楼受工厂B的“噪音影响度”与距离BP也成反比,比例系数是4.办公楼受A,B两厂的“总噪音影响度”y是受A,B两厂“噪音影响度”的和,设AP=xkm. (1)求“总噪音影响度” y关于x的函数关系式,并指出函数的定义域;
(1)求“总噪音影响度” y关于x的函数关系式,并指出函数的定义域; 如图,两个工厂A,B相距2
如图,两个工厂A,B相距2