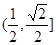题目内容
若x为三角形中的最小内角,则函数y=sinx+cosx的值域是( )
A、[
| ||||||
B、(0,
| ||||||
C、(1,
| ||||||
D、(
|
分析:由x为三角形中的最小内角,可得0<x≤
而y=sinx+cosx=
sin(x+
),结合已知所求的x的范围可求y的范围.
| π |
| 3 |
| 2 |
| π |
| 4 |
解答:解:因为x为三角形中的最小内角,
所以0<x≤
y=sinx+cosx=
sin(x+
)
∴
<
+x≤
<sin(x+
)≤1
1<y≤
故选C
所以0<x≤
| π |
| 3 |
y=sinx+cosx=
| 2 |
| π |
| 4 |
∴
| π |
| 4 |
| π |
| 4 |
| 7π |
| 12 |
| ||
| 2 |
| π |
| 4 |
1<y≤
| 2 |
故选C
点评:本题主要考查了辅助角公式的应用,正弦函数的部分图象的性质,属于基础试题.

练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
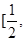
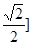 B.
B.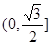 C.
C.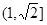 D.
D.