题目内容
 如图,已知平行六面体
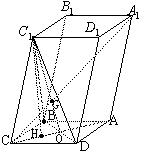
如图,已知平行六面体![]() 的底面ABCD是菱形,且
的底面ABCD是菱形,且![]() ,(1)证明:
,(1)证明: ![]() ;
;
(II)假定CD=2,![]() ,记面
,记面![]() 为α,面CBD为β,求二面角α -BD -β的平面角的余弦值;
为α,面CBD为β,求二面角α -BD -β的平面角的余弦值;
(III)当![]() 的值为多少时,能使
的值为多少时,能使![]() ?请给出证明.
?请给出证明.
(1)证明见解析。
(II)![]()
(III)当![]() 时,能使
时,能使![]() 。证明见解析。
。证明见解析。
解析:
(I)证明:连结![]() 、AC,AC和BD交于.,连结
、AC,AC和BD交于.,连结![]() , ∵四边形ABCD是菱形,∴AC⊥BD,BC=CD,
, ∵四边形ABCD是菱形,∴AC⊥BD,BC=CD, ![]() 可证
可证![]() ,
,![]() ,
,
故![]() ,但AC⊥BD,所以
,但AC⊥BD,所以![]() ,从而
,从而![]() ;
;
(II)解:由(I)知AC⊥BD,![]() ,
,![]()
![]() 是二面角α—BD—β的平面角,在
是二面角α—BD—β的平面角,在![]() 中,BC=2,
中,BC=2,![]() ,
,
![]() ,
,![]() ∵∠OCB=60°,
∵∠OCB=60°,![]() ,
,![]() ,故C1O=
,故C1O=![]() ,即C1O=C1C,作
,即C1O=C1C,作![]() ,垂足为H,∴点H是.C的中点,且
,垂足为H,∴点H是.C的中点,且![]() ,所以
,所以![]() ;
;
(III)当![]() 时,能使
时,能使![]()
证明一:∵![]() ,所以
,所以![]() ,又
,又![]() ,由此可得
,由此可得![]() ,∴三棱锥
,∴三棱锥![]() 是正三棱锥
是正三棱锥

练习册系列答案
相关题目
 如图,已知平行六面体OABC-O1A1B1C1,点G是上底面O1A1B1C1的中心,且
如图,已知平行六面体OABC-O1A1B1C1,点G是上底面O1A1B1C1的中心,且 如图,已知平行六面体ABC-A1B1C1的底面为正方形,O1,O分别为上、下底面中心,且A1在底面ABCD上的射影为O.
如图,已知平行六面体ABC-A1B1C1的底面为正方形,O1,O分别为上、下底面中心,且A1在底面ABCD上的射影为O. 如图,已知平行六面体ABCD-A1B1C1D1的底面为正方形,O1,O分别为上、下底面中心,且A1在底面ABCD上的射影为O.
如图,已知平行六面体ABCD-A1B1C1D1的底面为正方形,O1,O分别为上、下底面中心,且A1在底面ABCD上的射影为O. 如图,已知平行六面体ABCD-A1B1C1D1(底面是平行四边形的四棱柱)
如图,已知平行六面体ABCD-A1B1C1D1(底面是平行四边形的四棱柱) 如图,已知平行六面体ABCD-A1B1C1D1的底面为正方形,O1,O分别为上、下底面的中心,且A1在底面ABCD上的射影是O.
如图,已知平行六面体ABCD-A1B1C1D1的底面为正方形,O1,O分别为上、下底面的中心,且A1在底面ABCD上的射影是O.