题目内容
【题目】已知cosα= 
，cos（αβ）= 
，且0＜β＜α＜ 
，
（1）求tan2α的值；
（2）求β．
【答案】
（1）解：由cosα= 
，0＜β＜α＜ 
，可得sinα= 
= 
，tanα= 
=4 
，
∴tan2α= 
= 
= 
．
（2）解：由cosα= ，cos（αβ）= 
，且0＜β＜α＜ ，可得sin（αβ）= 
= 
，
∴cosβ=cos[α（αβ）]=cosαcos（αβ）+sinαsin（αβ）
= 
+ 
= 
，
∴β= 
．
【解析】（1）由条件利用同角三角函数的基本关系，求得tanα的值，再利用二倍角的正切公式求得tan2α的值．（2）由条件求得sin（αβ）的值，利用两角差的余弦公式求得cosβ=cos[α（αβ）]的值，从而求得β的值．
【考点精析】本题主要考查了同角三角函数基本关系的运用和两角和与差的正切公式的相关知识点，需要掌握同角三角函数的基本关系：
；
;（3） 倒数关系：
；两角和与差的正切公式：
才能正确解答此题．
练习册系列答案
名校课堂系列答案
相关题目
【题目】下表是某厂的产量x与成本y的一组数据：
产量x（千件） | 2 | 3 | 5 | 6 |
成本y（万元） | 7 | 8 | 9 | 12 |
（Ⅰ）根据表中数据，求出回归直线的方程 
= 
x 
（其中 = 
， 
= 
﹣ 
）
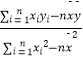（Ⅱ）预计产量为8千件时的成本．
