题目内容
如图,平面中两条直线l 1 和l 2相交于点O,对于平面上任意一点M,若x , y分别是M到直线l1和l2的距离,则称有序非负实数对(x , y)是点M的“距离坐标 ” 。
已知常数p≥0, q≥0,给出下列三个命题:
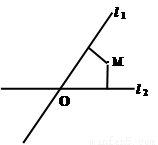
①若p=q=0,则“距离坐标”为(0,0)的点有且只有1个;
②若pq="0," 且p+q≠0,则“距离坐标”为( p, q) 的点有且只有2个;
③ 若pq≠0则“距离坐标”为 ( p, q) 的点有且只有4个.
上述命题中,正确命题的是 .(写出所有正确命题的序号)
【答案】
①②③
【解析】
试题分析:题目中点到直线的距离,分别为p、q,由于p、q的范围是常数p≥0,q≥0,所以对p、q进行分类讨论,验证①②③是否成立
解:①p=q=0,则“距离坐标”为(0,0)的点有且只有1个,此点为点O.故①正确;
②正确,p,q中有且仅有一个为0,当p为0时,坐标点在L1上,分别为关于O点对称的两点,反则在L2上也有两点,但是这两种情况不能同时存在;
③正确,四个交点为与直线l1相距为p的两条平行线和与直线l2相距为q的两条平行线的交点;
故答案为:①②③.
考点:本试题考查了新定义的运用。
点评:对于有创新试题的求解关键是理解题意,运用新的概念结合我们所学的知识来解答,,注意变形去掉p≥0,q≥0又该怎样解.属于中档题。

练习册系列答案
相关题目
 12、如图,平面中两条直线l1和l2相交于点O,对于平面上任意一点M,若p,q分别是M到直线l1和l2的距离,则称有序非负实数对(p,q)是点M的“距离坐标”,根据上述定义,“距离坐标”是(1,2)的点的个数是
12、如图,平面中两条直线l1和l2相交于点O,对于平面上任意一点M,若p,q分别是M到直线l1和l2的距离,则称有序非负实数对(p,q)是点M的“距离坐标”,根据上述定义,“距离坐标”是(1,2)的点的个数是 10、如图,平面中两条直线l1和l2相交于点O,对于平面上任意一点M,若p、q分别是M到直线l1和l2的距离,则称有序非负实数对(p,q)是点M的“距离坐标”.已知常数p≥0,q≥0,给出下列命题:
10、如图,平面中两条直线l1和l2相交于点O,对于平面上任意一点M,若p、q分别是M到直线l1和l2的距离,则称有序非负实数对(p,q)是点M的“距离坐标”.已知常数p≥0,q≥0,给出下列命题: 如图,平面中两条直线l1和l2相交于点O,对于平面上任意一点M,若p、q分别是M到直线l1和l2的距离,则称有序非负实数对(p,q)是点M的“距离坐标”.已知常数p≥0,q≥0,给出下列命题①若p=q=0,则“距离坐标”为(0,0)的点有且仅有1个;
如图,平面中两条直线l1和l2相交于点O,对于平面上任意一点M,若p、q分别是M到直线l1和l2的距离,则称有序非负实数对(p,q)是点M的“距离坐标”.已知常数p≥0,q≥0,给出下列命题①若p=q=0,则“距离坐标”为(0,0)的点有且仅有1个; 如图,平面中两条直线l1和l 2相交于点O,对于平面上任意一点M,若x,y分别是M到直线l 1和l 2的距离,则称有序非负实数对(x,y)是点M的“距离坐标”.已知常数p≥0,q≥0,给出下列三个命题:
如图,平面中两条直线l1和l 2相交于点O,对于平面上任意一点M,若x,y分别是M到直线l 1和l 2的距离,则称有序非负实数对(x,y)是点M的“距离坐标”.已知常数p≥0,q≥0,给出下列三个命题: 如图,平面中两条直线l1和l2相交于点O,对于平面上任意一点M,若x,y分别是M到直线l1和l2的距离,则称有序非负实数对(x,y)是点M的“距离坐标”.已知常数p≥0,q≥0,给出下列三个命题:
如图,平面中两条直线l1和l2相交于点O,对于平面上任意一点M,若x,y分别是M到直线l1和l2的距离,则称有序非负实数对(x,y)是点M的“距离坐标”.已知常数p≥0,q≥0,给出下列三个命题: