题目内容
（本题满分14分）已知数列
中，
,
，
（1）
证明：
是等比数列；
（2）若数列的前
项和为
，求数列
的通项公式，并求出n为何值时，取得最小值，并说明理由。（参考数据：
）
中，,，（1）
证明：是等比数列；（2）若数列
的前项和为，求数列的通项公式，并求出n为何值时，取得最小值，并说明理由。（参考数据：）（ 14分）
解：(1)∵，所以
，…………2分
又a1-1=-15≠0，所以数列{an-1}是等比数列； ……………4分
(2) 由(1)知：
，得
， ……………6分
从而
(nÎN*)； ………………………………8分
解不等式Sn<Sn+1， 得
，…………………………………9分
，…………………………………………………11分
当
n≥15时，数列{Sn}单调递增；
同理可得，当n≤15时，数列{Sn}单调递减；…………………………13分
故当n=15时，Sn取得最小值．…………………………………………14分
解：(1)∵，所以，…………2分又a1-1=-15≠0，所以数列{an-1}是等比数列； ……………4分
(2) 由(1)知：
，得， ……………6分从而
(nÎN*)； ………………………………8分解不等式Sn<Sn+1， 得
，…………………………………9分，…………………………………………………11分当
n≥15时，数列{Sn}单调递增；同理可得，当n≤15时，数列{Sn}单调递减；…………………………13分
故当n=15时，Sn取得最小值．…………………………………………14分
略
练习册系列答案
名校课堂系列答案
相关题目
中，
，若对任意的正整数
，当
时，不等
恒成立，求实数
的取值范围.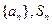
是其前
项和，且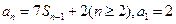
．
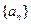的通项公式；
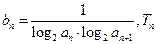是数列
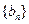的前
，求T10的值
}中，
求{
是等差数列｛
｝的前n项和，已知
=3，
=11，则
等于_________________
的前n项和为
，且
，
（n∈
），则
的
中，前n项的和为
，若
，则
中，
,
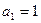，则前6项和为_________