题目内容
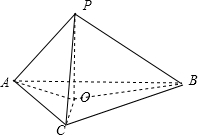
过三角形ABC所在平面α外一点P，作PO⊥α，垂足为O，连接PA，PB，PC．若PA⊥PB，PB⊥PC，PC⊥PA，则点O是三角形ABC的
垂
垂
心．分析：利用线线垂直，证明线面垂直，从而可得线线垂直，即可得O为△ABC的垂心
解答：解：连接AO，BO，CO
因为PA⊥PB，PA⊥PC，PB∩PC=P，所以PA⊥平面PBC
所以PA⊥BC
因为PO⊥平面ABC，所以PO⊥BC
因为PO∩PA=P，∴所以BC⊥平面PAO
所以BC⊥AO
同理BO⊥AC，CO⊥AB
∴O为△ABC的垂心
故答案为：垂心，
因为PA⊥PB，PA⊥PC，PB∩PC=P，所以PA⊥平面PBC
所以PA⊥BC
因为PO⊥平面ABC，所以PO⊥BC
因为PO∩PA=P，∴所以BC⊥平面PAO
所以BC⊥AO
同理BO⊥AC，CO⊥AB
∴O为△ABC的垂心
故答案为：垂心，
点评：本题综合考查线面垂直的判定与性质，掌握线面垂直的判定与性质是关键．
练习册系列答案
相关题目
外一点P，作PO
,垂足为O，连接PA,PB,PC.若PA
PB,PB