题目内容
对于函数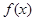 若存在
若存在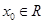 ,使得
,使得 成立,则称
成立,则称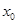 为
为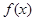 的不动点.
的不动点.
已知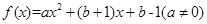
(1)当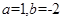 时,求函数
时,求函数 的不动点;
的不动点;
(2)若对任意实数 ,函数
,函数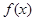 恒有两个相异的不动点,求
恒有两个相异的不动点,求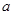 的取值范围;
的取值范围;
(3)在(2)的条件下,若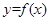 图象上
图象上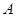 、
、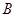 两点的横坐标是函数
两点的横坐标是函数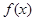 的不动点,且
的不动点,且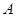 、
、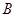 两点关于直线
两点关于直线 对称,求
对称,求 的最小值.
的最小值.
【答案】
(1)-1和3;(2)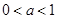 ;(3)
;(3)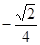 .
.
【解析】
试题分析:(1)根据不动点的定义,本题实质是求方程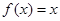 即
即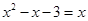 的解;(2)函数
的解;(2)函数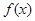 恒有两个相异的不动点即方程
恒有两个相异的不动点即方程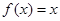 恒有两个不等实根,对应的判别式
恒有两个不等实根,对应的判别式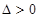 恒成立;(3)
恒成立;(3)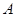 、
、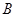 两点关于直线
两点关于直线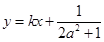 对称,可用的结论有:①直线AB与直线
对称,可用的结论有:①直线AB与直线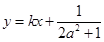 垂直,即斜率互为负倒数;②线段AB的中点在直线
垂直,即斜率互为负倒数;②线段AB的中点在直线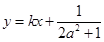 上.注意不动点A、B所在直线AB的斜率为1.
上.注意不动点A、B所在直线AB的斜率为1.
试题解析: (1)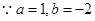 时,
时,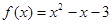 ,
,
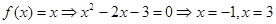
 函数
函数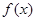 的不动点为-1和3;
的不动点为-1和3;
(2)即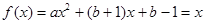 有两个不等实根,转化为
有两个不等实根,转化为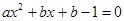 有两个不等实根,需有判别式大于0恒成立
有两个不等实根,需有判别式大于0恒成立
即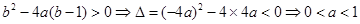 ,
,
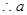 的取值范围为
的取值范围为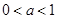 ;
;
 (3)设
(3)设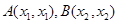 ,则
,则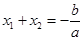 ,
,
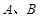 的中点
的中点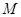 的坐标为
的坐标为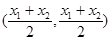 ,即
,即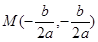
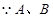 两点关于直线
两点关于直线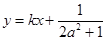 对称,
对称,
又因为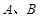 在直线
在直线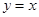 上,
上, 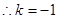 ,
,
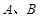 的中点
的中点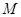 在直线
在直线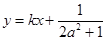 上,
上,
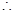
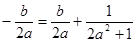
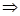
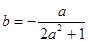
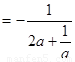
利用基本不等式可得当且仅当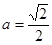 时,b的最小值为
时,b的最小值为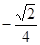 .
.
考点:(1)解方程;(2)二次方程有两个不等实根的条件;(3)直线的对称点问题及最小值问题.

练习册系列答案
相关题目
 若存在
若存在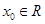 ,使得
,使得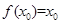 成立,则称
成立,则称 为
为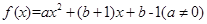
 时,求函数
时,求函数 的不动点;
的不动点;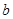 ,函数
,函数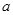 的取值范围;
的取值范围;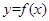 图象上
图象上 、
、 两点的横坐标是函数
两点的横坐标是函数 对称,求
对称,求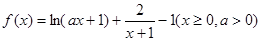 .
.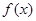 在
在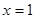 处取得极值,求
处取得极值,求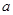 的值;
的值;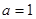 且
且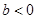 ,函数
,函数 ,若对于
,若对于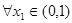 ,总存在
,总存在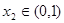 使得
使得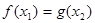 ,求实数
,求实数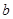 的取值范围.
的取值范围.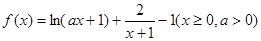 。
。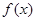 在
在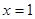 处取得极值,求
处取得极值,求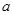 的值;
的值;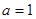 且
且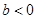 ,函数
,函数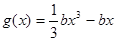 ,若对于
,若对于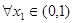 ,总存在
,总存在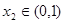 使得
使得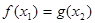 ,求实数
,求实数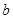 的取值范围。
的取值范围。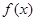 ,若存在实数对(
,若存在实数对(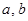 ),使得等式
),使得等式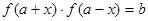 对定义域中的每
对定义域中的每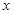 都成立,则称函数
都成立,则称函数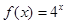 是否为“(
是否为“(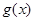 是“(1,4)型函数”, 当
是“(1,4)型函数”, 当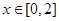 时,都有
时,都有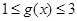 成立,且当
成立,且当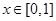
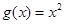
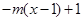
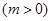 ,若,试求
,若,试求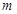 的取值范围.
的取值范围.