题目内容
（本题满分10分）
如图，ABCD是边长为2的正方形，O是正方形的中心，PO
底面ABCD，PO=
，E是PC的中点。
求证：（1）PA∥平面BDE；（2）直线PA与平面PBD所成的角.
【答案】
解: 证明（Ⅰ）∵O是AC的中点，E是PC的中点，∴OE∥AP，又∵OE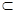
平面BDE，PA
平面BDE，∴PA∥平面BDE．
（Ⅱ）连接AC∵PO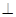
底面ABCD，∴PO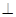AC，又∵AC
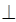BD，且BD
PO=O
∴AC平面PBD，∴∠APO即为所求角，
∵
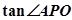=AO/PO=
/
=
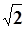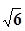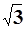/3；∴
=300
【解析】略
练习册系列答案
黎明文化寒假作业系列答案
寒假天地重庆出版社系列答案
相关题目
的图象在y轴上的截距为
，相邻的两个最值点是
和
（1）求函数
；（2）设
，问将函数
的图像？（3）画出函数
上的简图．
，求证：
；
，求证：三数
，
，
中至少有一个不小于2.
的所有棱长都为2，
为棱
的中点，
平面
；
的余弦值大小.
与
的距离，由于地形的限制，需要在岸上选取
和
两点，现测得
，
，
，
，
，求两景点