题目内容
已知椭圆C1: (a>b>0)的右顶点A(1,0),过C1的焦点且垂直长轴的弦长为1.
(a>b>0)的右顶点A(1,0),过C1的焦点且垂直长轴的弦长为1.(1)求椭圆C1的方程;
(2)设点P在抛物线C2:y=x2+h(h∈R)上,C2在点P处的切线与C1交于点M,N.若存在点P,使得线段AP的中点与MN的中点的横坐标相等时,求h的取值范围.
【答案】分析:(1)由椭圆右顶点A(1,0),过C1的焦点且垂直长轴的弦长为1,建立方程组,即可求出椭圆方程;
(2)不妨设 ,求出直线MN的方程代入椭圆C1的方程,根据直线MN与椭圆C1有两个不同的交点,所以有△>0,利用线段AP的中点与MN的中点的横坐标相等,建立方程,从而可得h的取值范围.
,求出直线MN的方程代入椭圆C1的方程,根据直线MN与椭圆C1有两个不同的交点,所以有△>0,利用线段AP的中点与MN的中点的横坐标相等,建立方程,从而可得h的取值范围.
解答:解:(1)由题意得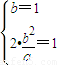 ,∴
,∴ ,…(3分)
,…(3分)
∴所求的椭圆方程为 …(5分)
…(5分)
(2)不妨设 ,则抛物线C2在点P处的切线斜率为y'|x=t=2t,…(6分)
,则抛物线C2在点P处的切线斜率为y'|x=t=2t,…(6分)
∴直线MN的方程为y=2tx-t2+h,代入椭圆C1的方程中,得4x2+(2tx-t2+h)2-4=0,
即4(1+t2)x2-4t(t2-h)x+(t2-h)2-4=0,…(7分)
因为直线MN与椭圆C1有两个不同的交点,所以有△=16t2(t2-h)2-16(1+t2)[(t2-h)2-4]>0
即-(t2-h)2+4+4t2>0,…(8分)
设线段MN的中点的横坐标是x3,则 ,
,
设线段PA的中点的横坐标是x4,则 ,
,
由题意得x3=x4,即有t2+(1+h)t+1=0,显然t≠0
∴ (t≠0)…(9分)
(t≠0)…(9分)
∴t4+2t3-2t2+2t+1<0,即(t2+t+1)2-5t2<0
解得
而
又 在
在 上递增,
上递增,
在 上递减…(11分)
上递减…(11分)
∴当t=-1时,h取到最小值1;…(12分)
当 或
或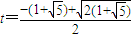 时,h的值都为
时,h的值都为
∴h的取值范围是 …(13分)
…(13分)
点评:本题考查椭圆的标准方程与性质,考查抛物线的切线,考查直线与椭圆的位置关系,考查学生分析解决问题的能力,考查计算能力,属于中档题.
(2)不妨设
 ,求出直线MN的方程代入椭圆C1的方程,根据直线MN与椭圆C1有两个不同的交点,所以有△>0,利用线段AP的中点与MN的中点的横坐标相等,建立方程,从而可得h的取值范围.
,求出直线MN的方程代入椭圆C1的方程,根据直线MN与椭圆C1有两个不同的交点,所以有△>0,利用线段AP的中点与MN的中点的横坐标相等,建立方程,从而可得h的取值范围.解答:解:(1)由题意得
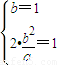 ,∴
,∴ ,…(3分)
,…(3分)∴所求的椭圆方程为
 …(5分)
…(5分)(2)不妨设
 ,则抛物线C2在点P处的切线斜率为y'|x=t=2t,…(6分)
,则抛物线C2在点P处的切线斜率为y'|x=t=2t,…(6分)∴直线MN的方程为y=2tx-t2+h,代入椭圆C1的方程中,得4x2+(2tx-t2+h)2-4=0,
即4(1+t2)x2-4t(t2-h)x+(t2-h)2-4=0,…(7分)
因为直线MN与椭圆C1有两个不同的交点,所以有△=16t2(t2-h)2-16(1+t2)[(t2-h)2-4]>0
即-(t2-h)2+4+4t2>0,…(8分)
设线段MN的中点的横坐标是x3,则
 ,
,设线段PA的中点的横坐标是x4,则
 ,
,由题意得x3=x4,即有t2+(1+h)t+1=0,显然t≠0
∴
 (t≠0)…(9分)
(t≠0)…(9分)∴t4+2t3-2t2+2t+1<0,即(t2+t+1)2-5t2<0
解得

而

又
 在
在 上递增,
上递增,在
 上递减…(11分)
上递减…(11分)∴当t=-1时,h取到最小值1;…(12分)
当
 或
或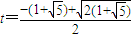 时,h的值都为
时,h的值都为
∴h的取值范围是
 …(13分)
…(13分)点评:本题考查椭圆的标准方程与性质,考查抛物线的切线,考查直线与椭圆的位置关系,考查学生分析解决问题的能力,考查计算能力,属于中档题.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
 (a>b>0)的左焦点为F1(-1,0),且点P(0,1)在C1上.
(a>b>0)的左焦点为F1(-1,0),且点P(0,1)在C1上. (a>b>0)的左焦点为F1(-1,0),且点P(0,1)在C1上.
(a>b>0)的左焦点为F1(-1,0),且点P(0,1)在C1上. (a>b>0)的左焦点为F1(-1,0),且点P(0,1)在C1上.
(a>b>0)的左焦点为F1(-1,0),且点P(0,1)在C1上. (a>b>0)的左、右顶点分别是A、B,P是双曲线C2:
(a>b>0)的左、右顶点分别是A、B,P是双曲线C2: =1右支x轴上方的一点,连接AP交椭圆于点C,连接PB并延长交椭圆于点D.
=1右支x轴上方的一点,连接AP交椭圆于点C,连接PB并延长交椭圆于点D.