题目内容
【题目】已知![]()
![]() 为椭圆
为椭圆![]() 上一点,
上一点,![]() 分别为
分别为![]() 关于
关于![]() 轴,原点,
轴,原点,![]() 轴的对称点,
轴的对称点,
(1)求四边形![]() 面积的最大值;
面积的最大值;
(2)当四边形![]() 最大时,在线段
最大时,在线段![]() 上任取一点
上任取一点![]() ,若过
,若过![]() 的直线与椭圆相交于
的直线与椭圆相交于![]() 两点,且
两点,且![]() 中点恰为
中点恰为![]() ,求直线
,求直线![]() 斜率
斜率![]() 的取值范围.
的取值范围.
【答案】(1)8 (2)![]()
【解析】
(1)由题意表示出![]() 点的坐标,即可用
点的坐标,即可用![]() 的式子表示四边形
的式子表示四边形![]() 面积,
面积,
因![]() 在椭圆上得
在椭圆上得![]() ,利用基本不等式即可求出面积的最大值。
,利用基本不等式即可求出面积的最大值。
(2)由(1)得![]() ,
,![]() ,设
,设![]() 点坐标为
点坐标为![]() ,利用点差法表示出直线
,利用点差法表示出直线![]() 的斜率,即可求出斜率
的斜率,即可求出斜率![]() 的取值范围。
的取值范围。
(1)由题意![]()
![]() ,
,![]() 分别为
分别为![]() 关于
关于![]() 轴,原点,
轴,原点,![]() 轴的对称点,
轴的对称点,
则![]() ,
,![]() ,
,![]() 则
则![]() 、
、![]() ,
,
![]()
由![]() 在椭圆上得
在椭圆上得![]()
∴![]() ,当
,当![]() 时取等号
时取等号
故当![]() ,
,![]() 时,四边形
时,四边形![]() 取最大值8
取最大值8
(2)由(1)得![]() ,
,![]() ,则
,则![]() 的坐标设为
的坐标设为![]() ,其中
,其中![]()
设![]() ,
,![]() ,则有
,则有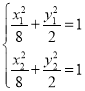 ,
,
相减得![]()
∵![]() 为
为![]() 中点,∴
中点,∴![]() ,
,![]()
∴上式化为![]() ,∴
,∴![]()
故![]()

【题目】为了解某班学生喜好体育运动是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
喜好体育运动 | 不喜好体育运动 | 合计 | |
男生 | 5 | ||
女生 | 10 | ||
合计 | 50 |
已知按喜好体育运动与否,采用分层抽样法抽取容量为10的样本,则抽到喜好体育运动的人数为6.
(1)请将上面的列联表补充完整;
(2)能否在犯错概率不超过0.01的前提下认为喜好体育运动与性别有关?说明理由.
附:![]()
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
【题目】为检查某工厂所生产的8万台电风扇的质量,随机抽取20台,其无故障连续使用时限(单位:h)统计如下:
分组 | 频数 | 频率 | 频率/组距 |
| 1 | 0.05 | 0.0025 |
| 1 | 0.05 | 0.0025 |
| 2 | 0.10 | 0.0050 |
| 3 | 0.15 | 0.0075 |
| 4 | 0.20 | 0.0100 |
| 6 | 0.30 | 0.0150 |
| 2 | 0.10 | 0.0050 |
| 1 | 0.05 | 0.0025 |
合计 | 20 | 1 | 0.050 |
(1)作出频率分布直方图;
(2)估计8万台电风扇中无故障连续使用时限不低于280h的有多少台;
(3)假设同一组中的数据用该组区间的中点值代替,估计这8万台电风扇的平均无故障连续使用时限.

